Question

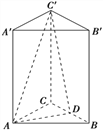
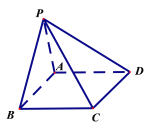
【题目】在四棱锥中，底面为正方形，已知，，，.

（1）证明：面；

（2）求二面角的大小.

Answer 1

【答案】（1）证明见解析（2）.

【解析】

(1)根据勾股定理证明,再结合证明即可.

(2) 过点作于,过作于,连结,再证明是二面角的平面角,再计算得即可求出的大小.

解：（1）证明：在中,由题设,,,,

可得,所以,

在正方形中,,

又,

又因为平面，

∴平面.

（2）过点作于,过作于,连结,

∵平面,平面,∴,

又,∴平面,

又平面,∴,

又,∴平面,

平面,∴,

∴是二面角的平面角.

由题可得,,,

中,,∴,

故二面角的大小为.

[Failed to download image : http://192.168.0.10:8086/QBM/2020/4/30/2452887117914112/2453859651313664/EXPLANATION/5ee163ab191742ff9ebf6fa427e52c26.png]