题目内容
【题目】如图,已知圆![]() 与
与![]() 轴的左右交点分别为
轴的左右交点分别为![]() ,与
,与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .
.
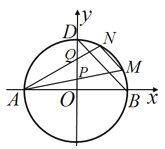
(1)若直线![]() 过点
过点![]() 并且与圆
并且与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若点![]() 是圆
是圆![]() 上第一象限内的点,直线
上第一象限内的点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先验证当直线斜率不存在时,可知满足题意;当直线斜率不存在时,假设直线方程,利用![]() 构造方程可求得切线斜率,从而得到结果;(2)假设直线
构造方程可求得切线斜率,从而得到结果;(2)假设直线![]() 方程,与圆的方程联立可求得
方程,与圆的方程联立可求得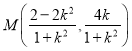 ;求出直线
;求出直线![]() 斜率后,可得
斜率后,可得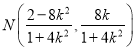 ,利用
,利用![]() 可知
可知![]() ,从而构造方程可求得直线
,从而构造方程可求得直线![]() 的斜率.
的斜率.
(1)当斜率不存在时,直线方程为:![]() ,与圆相切,满足题意
,与圆相切,满足题意
当斜率存在时,设切线方程为:![]() ,即:
,即:![]()
由直线与圆相切得:![]() ,即:
,即:![]() ,解得:
,解得:![]()
![]() 切线方程为:
切线方程为:![]() ,即:
,即:![]()
综上所述,切线方程为:![]() 或
或![]()
(2)由题意易知直线![]() 的斜率存在
的斜率存在
故设直线![]() 的方程为:
的方程为:![]() ,
,![]()
由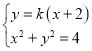 消去
消去![]() 得:
得:![]()
![]()
![]() ,代入
,代入![]() 得:
得:![]()
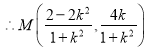
在![]() 中,令
中,令![]() 得:
得:![]()
![]() 点
点![]() 是线段
是线段![]() 的中点
的中点 ![]()
![]()
在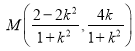 中,用
中,用![]() 代
代![]() 得:
得: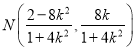
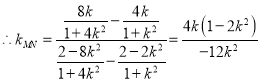
![]() 且
且![]()
![]()
即:![]() ,又
,又![]() ,解得:
,解得:![]()

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 |
|
|
|
| ||
频数 | 4 | 2 | 6 | 8 | ||
(1)请估计样本的平均数;
(2)以频率估计概率,若样本的容量为2000,求在分组![]() 中的频数;
中的频数;
(3)若从数据在分组![]() 与分组
与分组![]() 的样本中随机抽取2个,求恰有1个样本落在分组
的样本中随机抽取2个,求恰有1个样本落在分组![]() 的概率.
的概率.