题目内容
设函数f(x)=sin2ωx+2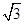
sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
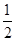,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(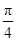
,0),求函数f(x)的值域.
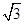sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(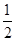,1).(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
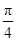,0),求函数f(x)的值域.(1) 
(2) [-2-
,2-]
(2) [-2-,2-]解:(1)f(x)=sin2ωx-cos2ωsinx+2
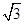sinωx·cosωx+λ=-cos2ωx+
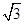sin2ωx+λ=2sin(2ωx-
)+λ.由直线x=π是y=f(x)图象的一条对称轴,
可得sin(2ωπ-
)=±1,所以2ωπ-
=kπ+
(k∈Z),即ω=
+
(k∈Z).又ω∈(
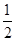,1),k∈Z,所以k=1,故ω=
.所以f(x)的最小正周期是
.(2)由y=f(x)的图象过点(
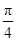,0),得f(
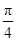)=0,即λ=-2sin(
×-)=-2sin
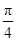=-,即λ=-
.故f(x)=2sin(
x-)-.所以函数f(x)的值域为[-2-
,2-].
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
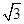,sinx),x∈R.
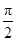),证明:a和b不平行;
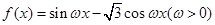的图象与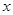
轴的两个相邻交点的距离等于
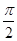，若将函数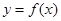
的图象向左平移
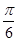个单位得到函数
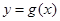的图象，则
-
sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
.
]上的最大值和最小值.
）在区间[0,
]上的最小值为( )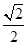
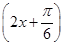＋2a＋b，当x∈
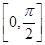时，－5≤f(x)≤1.
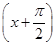且lgg(x)＞0，求g(x)的单调区间．
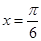是
的图象的一条对称轴，则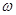
可以是（ ）
sinxcosx－cos2x＋
(x∈R)，则f(x)在区间
上的值域是________．
，下列选项正确的是 ( )
在
内是递增的