题目内容
7．设z=1-i（i为虚数单位），则z2+$\frac{2}{z}$的共轭复数是（ ）| A． | -1-i | B． | -1+i | C． | 1-i | D． | 1+i |
分析 把z=1-i代入z2+$\frac{2}{z}$，利用复数代数形式的乘除运算化简，然后利用共轭复数的概念得答案．
解答 解：∵z=1-i，∴z2+$\frac{2}{z}$=$（1-i）^{2}+\frac{2}{1-i}=-2i+\frac{2（1+i）}{（1-i）（1+i）}$=$-2i+\frac{2（1+i）}{2}=1-i$，
∴z2+$\frac{2}{z}$的共轭复数是1+i．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．
练习册系列答案
相关题目
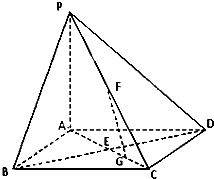如图，在底面是正方形的四棱锥P-ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一点．
2．设i为虚数单位，则|1-i|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |