题目内容
3．已知实数x，y满足$\left\{\begin{array}{l}x+y≥1\\{x^2}+{y^2}≤1\end{array}\right.$，则2x+y的取值范围是（ ）| A． | [1，2] | B． | [1，+∞） | C． | $（0，\sqrt{5}]$ | D． | $[1，\sqrt{5}]$ |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，即可求z的取值范围．
解答 解：设2x+y=b，则只需求直线2x+y=b在y轴上的截距范围．
画出可行域为弓形，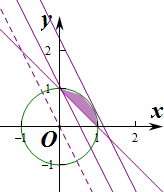
当直线与圆相切时，截距最大，且为$\sqrt{5}$，
当直线过点（0，1）时截距最小，且为1，
所以2x+y的取值范围是[1，$\sqrt{5}$]．
故选：D
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
蓝天教育暑假优化学习系列答案
相关题目
13．函数y=x4（2-x2）（0＜x＜$\sqrt{2}$）的最大值是（ ）
| A． | 0 | B． | 1 | C． | $\frac{16}{27}$ | D． | $\frac{32}{27}$ |
14．已知α，β∈（$\frac{3π}{2}$，2π），满足tan（α+β）-2tanβ=0，则tanα的最小值是（ ）
| A． | $\frac{{3\sqrt{2}}}{4}$ | B． | -$\frac{{\sqrt{2}}}{4}$ | C． | -$\frac{{3\sqrt{2}}}{4}$ | D． | $\frac{{\sqrt{2}}}{4}$ |