题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() 为
为![]() 的导函数.
的导函数.
(1)求方程![]() 的解集;
的解集;
(2)求函数![]() 的最大值与最小值;
的最大值与最小值;
(3)若函数![]() 在定义域上恰有2个极值点,求实数
在定义域上恰有2个极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为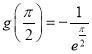 ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的知识建立方程求解;(2)借助题设运用导数的知识求解;(3)依据题设运用导数的知识分析探求.
试题解析:
(1)因为![]() ,................1分
,................1分
所以![]() ,解得
,解得![]() 或
或![]() ;...............3分
;...............3分
(2)因为![]() ,...........4分
,...........4分
令![]() ,解得
,解得![]() 或
或![]() ,...........................5分
,...........................5分
| 0 |
|
|
|
|
|
|
|
| 0 |
| 0 |
| ||
| 1 |
|
|
|
|
|
|
所以![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 的最小值为
的最小值为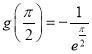 .........7分
.........7分
(3)因为![]() ,
,
所以函数![]() 在定义域上恰有2个极值点,等价于
在定义域上恰有2个极值点,等价于![]() 在定义域上恰有2个零点且在零点处异号,即
在定义域上恰有2个零点且在零点处异号,即![]() 与
与![]() 的图象恰有两个交点................... 9分
的图象恰有两个交点................... 9分
由(2)知![]() ,
,
![]() ,
,
若![]() ,则
,则![]() ,
,
所以![]() 至多只有1个零点,不成立,...............10分
至多只有1个零点,不成立,...............10分
所以只有![]() ;..................11分
;..................11分
若![]() ,则
,则![]() ,所以
,所以![]() 只有1个零点,不成立,..........12分
只有1个零点,不成立,..........12分
所以![]() ................13分
................13分
若![]() ,即
,即![]() ,在
,在![]() 处同号,不成立;
处同号,不成立;
若![]() ,则
,则![]() 有3个零点,不成立,....................14分
有3个零点,不成立,....................14分
所以只有![]() .
.
所以满足的条件为: ,
,
解得![]() 或
或![]() ....................16分
....................16分
注:利用图像直接得出![]() 或
或![]() 扣4分.
扣4分.

练习册系列答案
相关题目