Question

【题目】已知函数，其中.

（1）当时，求曲线在点处的切线方程；

（2）当时，求函数的单调区间与极值.

Answer 1

【答案】（1）（2）见解析

【解析】试题分析: （1）利用导数的几何意义:切线斜率等于,再根据点斜式求切线方程;(2)先明确函数的定义域,再求函数导数,研究导函数在定义域上的零点: 由，得,分类讨论两个零点的大小,再结合列表确定函数的单调区间与极值.

试题解析:（1）当时， ，此时，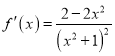

所以

又因为切点为，所以切线方程

曲线在点处的切线方程为

（2）由于，

所以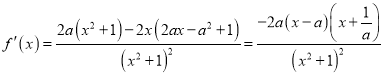

由，得

(1)当时，则，易得在区间， 内为减函数，

在区间为增函数，故函数在处取得极小值

函数在处取得极大值

当时，则,易得在区间， 内为增函数，

在区间为减函数，故函数在处取得极小值；

函数 在处取得极大值

点睛:本题考查导数的几何意义,属于基础题目. 函数y＝f(x)在x＝x0处的导数的几何意义，就是曲线y＝f(x)在点P(x0，y0)处的切线的斜率，过点P的切线方程为： .求函数y＝f(x)在点P(x0，y0)处的切线方程与求函数y＝f(x)过点P(x0，y0)的切线方程意义不同，前者切线有且只有一条，且方程为y－y0＝f′(x0)(x－x0)，后者可能不只一条．