题目内容
8.已知a为实数,函数f(x)=x3+|x-a|.(1)若a=0,求方程f(x)=x的解集;
(2)若函数y=f(x)在R上是增函数,求实数a的取值范围;
(3)若不等式f(x)≥1在[-1,1]上恒成立,求正实数a的最小值.
分析 (1)将a=0代入,再分当x≥0时和当x<0时去除绝对值符号,分别求解,最后综合讨论结果可得:方程f(x)=x的解集;
(2)若函数y=f(x)在R上是增函数,则f'(x)≥0恒成立,利用导数法可求实数a的取值范围;
(3)若不等式f(x)≥1在[-1,1]上恒成立,则|a-x|≥1-x3对一切x∈[-1,1]恒成立,即a≥-x3+x+1对一切x∈[-1,1]恒成立,构造函数h(x)=-x3+x+1利用导数求出函数的最值,可得正实数a的最小值.
解答 解:(1)a=0,f(x)=x,即x3+|x|=x.
当x≥0时,x3+x=x,
∴x=0. …(1分)
当x<0时,x3-x=x,
∴x2=2.则$x=-\;\sqrt{2}$. …(3分)
∴方程f(x)=x的解集为 { 0,$-\;\sqrt{2}$}. …(4分)
(2)$f(x)=\;\left\{\begin{array}{l}{x^3}+x-a,\;\;x\;≥\;a\\{x^3}-x+a,\;\;x\;<\;a.\end{array}\right.$
当x>a时,f'(x)=3x2+1>0恒成立,
∴f(x)在 (a,+∞) 上是增函数. …(6分)
当x<a时,f'(x)=3x2-1,当a≤$-\frac{{\sqrt{3}}}{3}$时,f'(x)=3x2-1≥0在(-∞,a )恒成立,
∴f(x)在 (-∞,a ) 上是增函数.
综上所述,a≤$-\frac{{\sqrt{3}}}{3}$. …(8分)
(3)f(x)≥1,即x3+|x-a|≥1,即|a-x|≥1-x3.
∵上式对一切x∈[-1,1]恒成立,
将x=-1代入,得|a+1|≥2,又a>0,
∴a≥1. …(10分)
则x3-x+a≥1,即a≥-x3+x+1对一切x∈[-1,1]恒成立. …(12分)
设函数h(x)=-x3+x+1,
∵h'(x)=-3x2+1,令h'(x)=0,得$x=±\frac{{\sqrt{3}}}{3}$.
| x | -1 | (-1,$-\frac{{\sqrt{3}}}{3}$) | $-\frac{{\sqrt{3}}}{3}$ | ($-\frac{{\sqrt{3}}}{3}$,$\frac{{\sqrt{3}}}{3}$) | $\frac{{\sqrt{3}}}{3}$ | ($\frac{{\sqrt{3}}}{3}$Z,1) | 1 |
| h'(x) | - | 0 | + | 0 | - | ||
| h(x) | 1 | ↘ | $1-\frac{{2\sqrt{3}}}{9}$ | ↗ | $1+\frac{{2\sqrt{3}}}{9}$ | ↘ | 1 |
∴$a≥\;1+\frac{{2\sqrt{3}}}{9}$时,a≥-x3+x+1对一切x∈[-1,1]恒成立.
∴正实数a的最小值为 $1+\frac{{2\sqrt{3}}}{9}$. …(16分)
点评 本题考查的知识点是分段函数的应用,利用导数法分析函数的单调性,利用导数法求函数的最值,恒成立问题,是导数与分段函数的综合应用,难度较大.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | 10 | B. | 8 | C. | -8 | D. | -10 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| A. | 4 | B. | 10 | C. | 20 | D. | 40 |
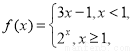 则满足
则满足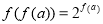 的
的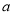 的取值范围是( )
的取值范围是( )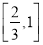 B.
B.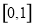
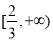 D.
D.