题目内容
【题目】下列说法错误的是( )
A.设p:f(x)=x3+2x2+mx+1是R上的单调增函数, ![]() ,则p是q的必要不充分条件
,则p是q的必要不充分条件
B.若命题 ![]() ,则¬p:?x∈R,x2﹣x+1>0
,则¬p:?x∈R,x2﹣x+1>0
C.奇函数f(x)定义域为R,且f(x﹣1)=﹣f(x),那么f(8)=0
D.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
【答案】A
【解析】解:对于A,f(x)=x3+2x2+mx+1是R上的单调增函数,则f′(x)=3x2+4x+m≥在R上恒成立,m≥(﹣3x2﹣4x)max , 即m ![]() ,∴p是q充要条件,故错;
,∴p是q充要条件,故错;
对于B,含有量词的命题的否定,先换量词,再否定结论,故正确;
对于C,奇函数f(x)定义域为R,由f(x﹣1)=﹣f(x)周期为2且f(0)=0,∴f(8)=0,故正确;
对于D,“x=y=0”的否定是x=0或y=0,故正确.
故选:A.
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 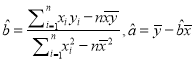 .
.
参考数据: ![]() .
.


