题目内容
已知函数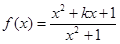 。
。
(Ⅰ)若当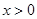 时,
时,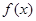 的最小值为-1,求实数k的值;
的最小值为-1,求实数k的值;
(Ⅱ)若对任意的 ,均存在以
,均存在以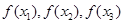 为三边边长的三角形,求实数k的取值范围。
为三边边长的三角形,求实数k的取值范围。
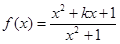 。
。(Ⅰ)若当
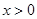 时,
时,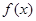 的最小值为-1,求实数k的值;
的最小值为-1,求实数k的值;(Ⅱ)若对任意的
 ,均存在以
,均存在以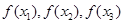 为三边边长的三角形,求实数k的取值范围。
为三边边长的三角形,求实数k的取值范围。(Ⅰ)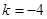 (Ⅱ)
(Ⅱ)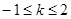
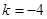 (Ⅱ)
(Ⅱ)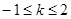
本试题主要是考查了导数在研究函数中的运用。以及不等式的综合运用。
(1)根据已知函数分子和分母配凑变形得到关于对勾函数的表达式,然后结合均值不等式得到最值。
(2)对于参数k进行分类讨论得到函数的不等式,进而的大大参数k的范围。
解:(Ⅰ)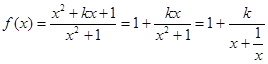 1分
1分
①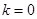 时,
时,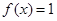 ,不合题意; 2分
,不合题意; 2分
②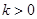 时,
时,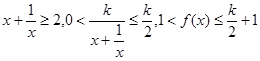 ,不合题意; 4分
,不合题意; 4分
③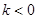 时,
时,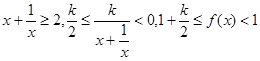 ,由题意,
,由题意,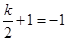 ,
,
所以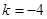 ; 6分
; 6分
(Ⅱ)①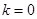 时,
时,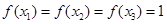 ,满足题意; 7分
,满足题意; 7分
②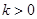 时,
时,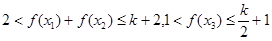 ,所以
,所以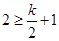 ,
,
即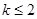 ,故
,故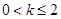 ; 9分
; 9分
③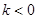 时,
时,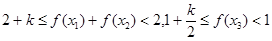 ,由题意,
,由题意,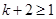 ,所以
,所以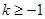 ,
,
故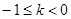 。综上可知,实数k的取值范围是
。综上可知,实数k的取值范围是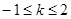 。 10分
。 10分
(1)根据已知函数分子和分母配凑变形得到关于对勾函数的表达式,然后结合均值不等式得到最值。
(2)对于参数k进行分类讨论得到函数的不等式,进而的大大参数k的范围。
解:(Ⅰ)
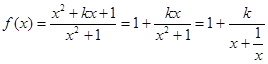 1分
1分①
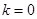 时,
时,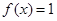 ,不合题意; 2分
,不合题意; 2分②
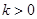 时,
时,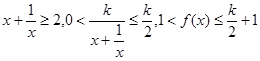 ,不合题意; 4分
,不合题意; 4分③
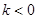 时,
时,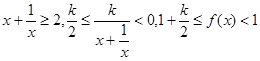 ,由题意,
,由题意,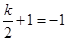 ,
,所以
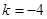 ; 6分
; 6分(Ⅱ)①
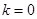 时,
时,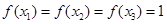 ,满足题意; 7分
,满足题意; 7分②
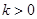 时,
时,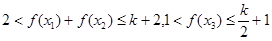 ,所以
,所以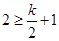 ,
,即
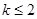 ,故
,故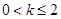 ; 9分
; 9分③
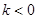 时,
时,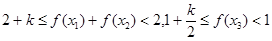 ,由题意,
,由题意,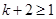 ,所以
,所以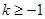 ,
,故
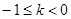 。综上可知,实数k的取值范围是
。综上可知,实数k的取值范围是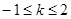 。 10分
。 10分
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
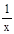
 -2x
-2x 
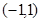 上的函数
上的函数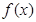 满足:
满足: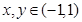 ,都有
,都有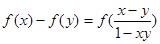 ;
; 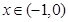 ,都有
,都有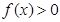 .
.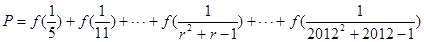 ,
,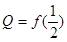 ,
,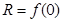 ,则
,则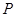 、
、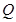 、
、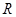 的大小关系为( )
的大小关系为( )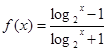 ,若
,若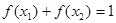 (其中
(其中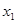 、
、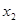 均大于2),则
均大于2),则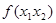 的最小值为 。
的最小值为 。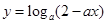 在[0,1]上单调递减,则实数a的取值范围是_________.
在[0,1]上单调递减,则实数a的取值范围是_________. 上的函数
上的函数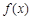 满足:对任意
满足:对任意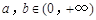 ,都有
,都有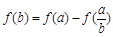 ,且当
,且当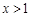 时,
时,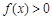 .
.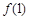 的值;
的值; ,解不等式
,解不等式 .
.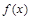 是定义在
是定义在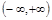 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足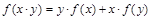 .
.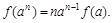 (
(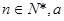 为不为零的常数)
为不为零的常数)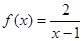 ,当
,当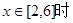 ,函数的最大值为
,函数的最大值为