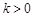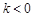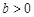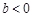题目内容
已知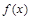 是定义在
是定义在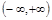 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足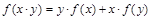 .
.
(1)求f (1)、f (-1)的值;
(2)判断f (x)的奇偶性,并说明理由;
(3)证明: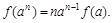 (
(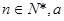 为不为零的常数)
为不为零的常数)
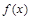 是定义在
是定义在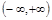 上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足
上的不恒为零的函数,且对定义域内的任意x, y, f (x)都满足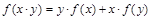 .
.(1)求f (1)、f (-1)的值;
(2)判断f (x)的奇偶性,并说明理由;
(3)证明:
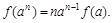 (
(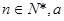 为不为零的常数)
为不为零的常数)(1)∴f (1)="0" ;f (-1)=0.(2)函数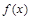 是
是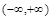 上的奇函数.
上的奇函数.
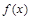 是
是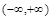 上的奇函数.
上的奇函数. 本试题主要是考查了函数的奇偶性和函数的赋值法思想的运用。
(1)根据已知条件,对于x,y赋值得到结论。令x=y=1时,有
(2)∵f(x)对任意x,y都有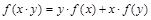
∴令x=t,y=-1,有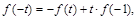
将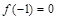 代入得
代入得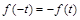
(3)对于难以用一般方法证明的自然数命题用数学归纳法证明即可
(1)根据已知条件,对于x,y赋值得到结论。令x=y=1时,有

(2)∵f(x)对任意x,y都有
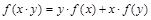
∴令x=t,y=-1,有
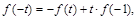
将
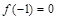 代入得
代入得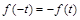
(3)对于难以用一般方法证明的自然数命题用数学归纳法证明即可

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
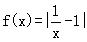
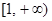 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;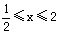 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;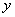 轴相交; ②定义在
轴相交; ②定义在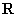 上的奇函数
上的奇函数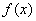 必满足
必满足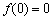 ;
;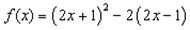 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;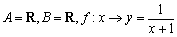 ,则
,则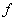 为
为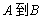 的映射;
的映射;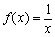 在
在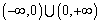 上是减函数.
上是减函数.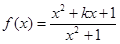 。
。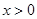 时,
时,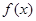 的最小值为-1,求实数k的值;
的最小值为-1,求实数k的值; ,均存在以
,均存在以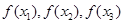 为三边边长的三角形,求实数k的取值范围。
为三边边长的三角形,求实数k的取值范围。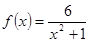
 的不等式
的不等式 的解集一切实数,求实数
的解集一切实数,求实数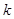 的取值范围;
的取值范围;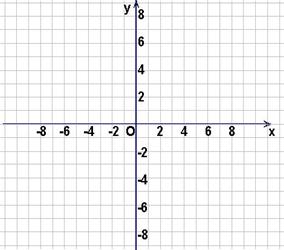
 ="(1,2),"
="(1,2)," 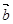 =(-2,1),k,t为正实数,向量
=(-2,1),k,t为正实数,向量  =
= 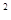 +1)
+1)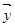 =-k
=-k
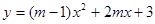 是偶函数,则
是偶函数,则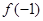 ,
, ,
,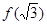 的大小关系为( )
的大小关系为( )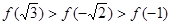
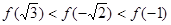
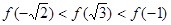
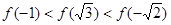
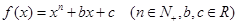
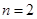 ,
,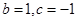 ,当
,当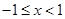 时,求
时,求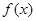 的单调区间和值域;
的单调区间和值域;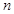 为偶数时,
为偶数时,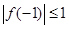 ,
,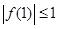 ,求
,求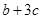 的最小值和最大值.
的最小值和最大值.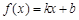 在R上单调递减,则( )
在R上单调递减,则( )