题目内容
2.在直角坐标系xOy中,圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2交点的直角坐标;
(Ⅱ)求圆C1与C2的公共弦所在直线的极坐标方程.
分析 (Ⅰ)利用极坐标与直角坐标的互化,求出圆C1,C2的极坐标方程,求出圆C1,C2交点的直角坐标;
(Ⅱ)利用圆C1与C2的解得的直角坐标,求出公共弦所在直线的极坐标方程.
解答 (本题满分10分) 选修4-4:极坐标与参数方程
解:(Ⅰ)圆C1的极坐标方程为ρ=2,
圆C2的极坐标方程ρ=4cosθ.
解$\left\{\begin{array}{l}ρ=2\\ ρ=4cosθ\end{array}$,得ρ=2,θ=±$\frac{π}{3}$,
故圆C1与圆C2交点的坐标为(2,$\frac{π}{3}$),(2,-$\frac{π}{3}$).
注:极坐标系下点的表示不唯一.
(Ⅱ)由$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}$,得圆C1与C2交点的直角坐标分别为(1,$\sqrt{3}$),(1,-$\sqrt{3}$).
故圆C1与C2的公共弦的参数方程为$\left\{\begin{array}{l}x=1\\ y=t\end{array}$,-$\sqrt{3}$≤t≤$\sqrt{3}$.
极坐标方程为:ρ=$\frac{1}{cosθ}$.
点评 本题考查极坐标与直角坐标方程的互化,考查转化思想以及计算能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.已知集合A={(x,y)|y=ex},B={(x,y)|y=a},若A∩B=∅,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<0 | D. | a≤0 |
10.已知函数f(x)和g(x)分别是定义在[-10,10]上的奇函数和偶函数,则函数F(x)=f(x)•g(x)的图象关于( )
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
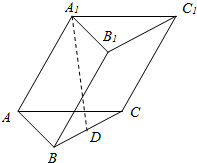 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.