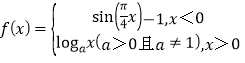题目内容
【题目】已知函数![]() .
.
(1)a=1时,求函数f(x)的极值;
(2)若![]() ,求f(x)的最小值g(a)的取值范围.
,求f(x)的最小值g(a)的取值范围.
【答案】(1)f(x)极小值e﹣1,无极大值;(2)[ln2﹣1,e﹣1].
【解析】
(1)代入![]() 求导可得
求导可得![]() ,再求导分析单调性与最值可知
,再求导分析单调性与最值可知![]() ,进而求得
,进而求得![]() 的极值点与单调区间以及极值.
的极值点与单调区间以及极值.
(2)求导后构造导函数![]() 得出
得出![]() ,再根据(1)中的结论可知
,再根据(1)中的结论可知![]() 恒成立,进而可得
恒成立,进而可得![]() 在定义域上单调递增.再根据零点存在定理可知
在定义域上单调递增.再根据零点存在定理可知![]() 在
在![]() 上有唯一解
上有唯一解![]() ,且
,且![]() ,进而求得最小值
,进而求得最小值![]() ,再根据隐零点问题消去参数
,再根据隐零点问题消去参数![]() ,再构造函数关于极值点
,再构造函数关于极值点![]() 的函数分析即可.
的函数分析即可.
(1)当a=1时,![]() ,则
,则![]() ,
,
令h(x)=ex﹣x,当x∈(0,+∞)时,h′(x)=ex﹣1>0,
∴在(0,+∞)上,h(x)>h(0)=1,即ex>x,
令f′(x)=0,则x=1,经检验,在(0,1)上,f′(x)<0,f(x)单调递减,在(1,+∞)上,f′(x)>0,f(x)单调递增,
∴当x=1时,函数y=f(x)取得极小值e﹣1,无极大值;
(2)![]() ,令
,令![]() ,
,
则![]() ,
,
由(1)知,当x∈(0,+∞)时,
ex>x,ex(x2﹣2x+2)﹣x>x(x2﹣2x+2)﹣x=x(x﹣1)2≥0,
∴p′(x)>0在(0,+∞)上恒成立,
∴f′(x)在定义域上单调递增,
∵![]() ,
,
∴![]() ,
,
∴方程f′(x)=0在(0,+∞)上有唯一解,
设方程f′(x)=0的解为x0,则在(0,x0)上f′(x)<0,在(x0,+∞)上f′(x)>0,且1≤x0≤2,
∴f(x)的最小值为![]() ,
,
由f′(x)=0得,![]() 代入g(a)得,
代入g(a)得,![]() ,
,
令![]() ,则
,则![]() ,
,
∵﹣x2+2x﹣2=﹣(x﹣1)2﹣1≤﹣1,
∴ex(﹣x2+2x﹣2)+x≤x﹣ex<0,
∴φ(x)在[1,2]上为减函数,
∴![]() ,
,
∴g(a)∈[ln2﹣1,e﹣1].

练习册系列答案
相关题目