题目内容
8.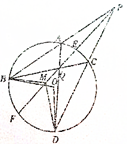 如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A、B、C、D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E、F,点M在EF上,且∠BAD=∠BMF.
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A、B、C、D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E、F,点M在EF上,且∠BAD=∠BMF.(1)求证:PA•PB=PM•PQ;
(2)求证:∠BMD=∠BOD.
分析 (1)利用AA,Q,M,B四点共圆,证明PA•PB=PM•PQ;
(2)利用△CPQ∽△MPD,证明∠BMD=∠BMF+∠DMF=2∠BAD,∠BOD=2∠BAD,即可证明∠BMD=∠BOD.
解答 证明:(1)∵∠BAD=∠BMF,
∴A,Q,M,B四点共圆,
∴PA•PB=PM•PQ.
(2)∵PA•PB=PC•PD,
∴PC•PD=PM•PQ,
又∠CPQ=∠MPD,
∴△CPQ∽△MPD,
∴∠PCQ=∠PMD,则∠DCB=∠FMD,
∵∠BAD=∠BCD,
∴∠BMD=∠BMF+∠DMF=2∠BAD,
又∠BOD=2∠BAD,
∴∠BMD=∠BOD.
点评 本题考查四点共圆,考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.在三角函数中,$\frac{8}{3}$π=( )
| A. | 270° | B. | 520° | C. | 480° | D. | 710° |