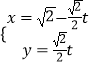题目内容
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).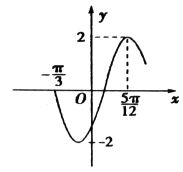
【答案】解:(Ⅰ)根据函数f(x)=Asin(ωx+φ)的图象知A=2.
∵ ![]() =
= ![]() ﹣(
﹣( ![]() ),∴T=π.∴ω=2.
),∴T=π.∴ω=2.
由五点法作图知当x= ![]() 时,ωx+φ=
时,ωx+φ= ![]() ,
,
即2× ![]() π+φ=
π+φ= ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .故
.故 ![]() .
.
(Ⅱ)先把y=sinx的图象向右平移 ![]() 个单位长度得到
个单位长度得到 ![]() 的图象,
的图象,
使曲线上各点的横坐标变为原来的 ![]() ,得到函数
,得到函数 ![]() 的图象,
的图象,
最后把曲线上各点的纵坐标变为原来的2倍,得到 ![]() .
.
(Ⅲ)由 ![]() 得
得 ![]() ,因为
,因为 ![]()
所以 ![]() ,得
,得 ![]() ,故
,故 ![]() ,
,
∴ 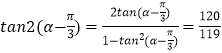 .
.
【解析】(1)根据函数图象可知A=2,由图象可读出最小正周期T=π,根据周期公式得到ω=2,又因为点(![]() ,2)在函数图象上,代入即可解出φ的值,从而得到f(x)的解析式,(2)通过函数图象的平移规则可得出平移过程,(3)根据f (
,2)在函数图象上,代入即可解出φ的值,从而得到f(x)的解析式,(2)通过函数图象的平移规则可得出平移过程,(3)根据f ( ![]() ) =
) = ![]() 得 s i n ( α
得 s i n ( α ![]() ) =
) = ![]() ,判断出α
,判断出α ![]() 的范围后,根据同角的三角函数关系得出cos(α
的范围后,根据同角的三角函数关系得出cos(α ![]() )的值,进而得到tan(α
)的值,进而得到tan(α ![]() ),结合二倍角的正切公式可得结果.
),结合二倍角的正切公式可得结果.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目