题目内容
【题目】等比数列{an}的各项都是正数,2a5 , a4 , 4a6成等差数列,且满足 ![]() ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ![]() ,n∈N* , 且b1=1
,n∈N* , 且b1=1
(1)求数列{an},{bn}的通项公式
(2)设 ![]() ,n∈N* , {Cn}前n项和为
,n∈N* , {Cn}前n项和为 ![]() ,求证:
,求证: ![]() .
.
【答案】
(1)解:设等比数列{an}的公比为q,由题意可知2a4=2a5+4a6,即a4=a4q+2a4q2,
由an>0,则2q2+q﹣1=0,解得:q= ![]() ,或q=﹣1(舍去),
,或q=﹣1(舍去),
a4=4a32=4a2a4,则a2= ![]() ,
,
∴a1= ![]() ,
,
等比数列{an}通项公式an=( ![]() )n,
)n,
当n≥2时,bn=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() ,
,
整理得: ![]() =
= ![]() ,
,
∴数列{ ![]() }是首项为
}是首项为 ![]() =1的常数列,
=1的常数列,
则 ![]() =1,则bn=n,n∈N*,
=1,则bn=n,n∈N*,
数列{bn}的通项公式bn=n,n∈N*
(2)解:证明:由(1)可知:cn= ![]() an
an
= ![]()
![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴ ![]() ck=c1+c2+…+cn=(
ck=c1+c2+…+cn=( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+
)+…+ ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]() <
< ![]() .
.
【解析】(1)由于数列{an}为等比数列,根据等比数列的通项公式表示出a4,a5,a6,根据2a5,a4,4a6成等差数列,可得2a4=2a5+4a6,可解得公比q,从而得到等比数列的通项公式,由bn=Sn﹣Sn﹣1,化简整理可得数列{bn}的通项公式,(2)由(1)求得数列{Cn}的通项公式,采用裂项相消即可求得数列{Cn}前n项和,即可证明不等式成立.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系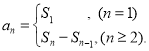 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

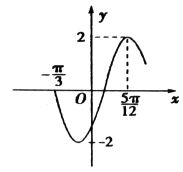
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |