题目内容
如图,椭圆的中心在原点,其左焦点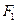 与抛物线
与抛物线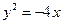 的焦点重合,过
的焦点重合,过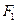 的直线
的直线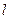 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线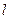 与x轴垂直时,
与x轴垂直时,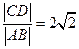 .
.
(Ⅰ)求椭圆的方程;
(II)求过点O、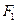 ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;
(Ⅲ)求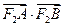 的最大值和最小值.
的最大值和最小值.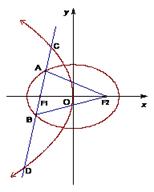
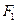 与抛物线
与抛物线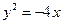 的焦点重合,过
的焦点重合,过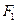 的直线
的直线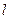 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线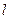 与x轴垂直时,
与x轴垂直时,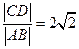 .
.(Ⅰ)求椭圆的方程;
(II)求过点O、
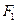 ,并且与椭圆的左准线相切的圆的方程;
,并且与椭圆的左准线相切的圆的方程;(Ⅲ)求
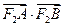 的最大值和最小值.
的最大值和最小值.
(Ⅰ)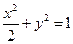
(Ⅱ)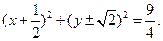
(Ⅲ)最大值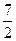 ,最小值
,最小值
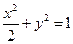
(Ⅱ)
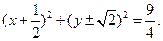
(Ⅲ)最大值
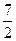 ,最小值
,最小值
(Ⅰ)由抛物线方程,得焦点
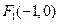 .
.设椭圆的方程:
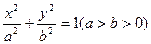 .
.解方程组
 得C(-1,2),D(1,-2).
得C(-1,2),D(1,-2).由于抛物线、椭圆都关于x轴对称,
∴
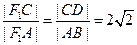 ,
,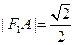 ,∴
,∴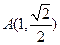 . …………2分
. …………2分∴
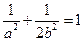 又
又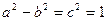 ,
,因此,
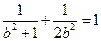 ,解得
,解得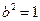 并推得
并推得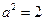 .
.故椭圆的方程为
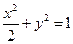 . …………4分
. …………4分(Ⅱ)
 ,
, 圆过点O、
圆过点O、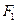 ,
, 圆心M在直线
圆心M在直线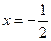 上.
上.设
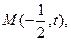 则圆半径,由于圆与椭圆的左准线相切,
则圆半径,由于圆与椭圆的左准线相切,∴
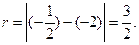
由
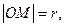 得
得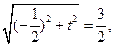 解得
解得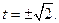
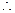 所求圆的方程为
所求圆的方程为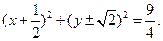 …………………………8分
…………………………8分(Ⅲ)由
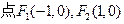
①若
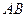 垂直于
垂直于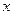 轴,则
轴,则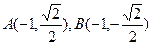 ,
,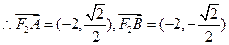 ,
,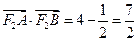 …………………………………………9分
…………………………………………9分②若
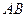 与
与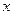 轴不垂直,设直线
轴不垂直,设直线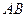 的斜率为
的斜率为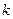 ,则直线
,则直线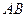 的方程为
的方程为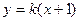
由
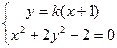 得
得 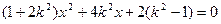
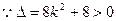 ,
, 方程有两个不等的实数根.
方程有两个不等的实数根.设
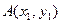 ,
,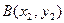 .
.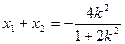 ,
, 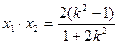 ………………………………11分
………………………………11分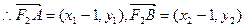
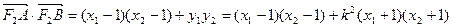
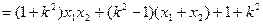
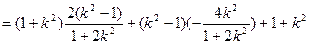
=
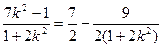
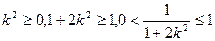
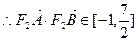 ,所以当直线
,所以当直线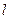 垂于
垂于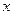 轴时,
轴时,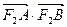 取得最大值
取得最大值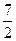
当直线
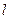 与
与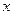 轴重合时,
轴重合时,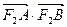 取得最小值
取得最小值

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
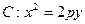 ,过点
,过点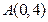 的直线
的直线 交抛物线
交抛物线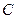 于
于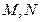 两点,且
两点,且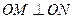 .
.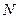 作
作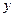 轴的平行线与直线
轴的平行线与直线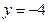 相交于点
相交于点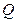 ,若
,若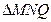 是等腰三角形,求直线
是等腰三角形,求直线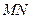 的方程.
的方程.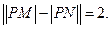
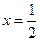 的距离,若
的距离,若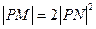 ,求
,求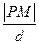 的值.
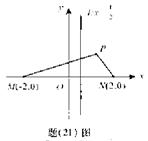
的值.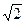 ),对应的准线方程为y=-
),对应的准线方程为y=-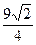 ,且离心率e满足:
,且离心率e满足: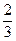 ,e,
,e,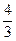 成等比数列.
成等比数列.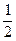
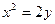 交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。
交于A、B两点,该抛物线在A、B两点处的两条切线交于点P。 (I)求点P的轨迹方程; (II)求△ABP的面积的最小值。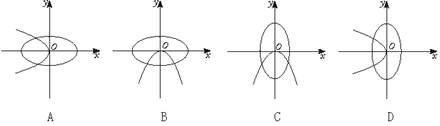
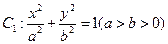 的左、右焦点分别为
的左、右焦点分别为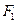 、
、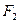 ,其中
,其中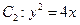 的焦点,
的焦点,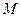 是
是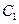 与
与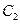 在第一象限的交点,且
在第一象限的交点,且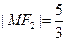 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆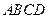 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆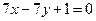 上,求直线
上,求直线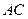 的方程.
的方程.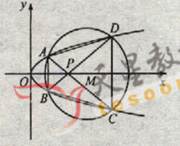 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线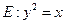
 与圆
与圆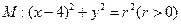 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。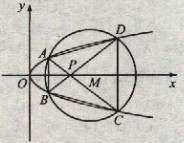
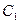 :
: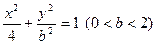 的离心率等于
的离心率等于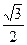 ,抛物线
,抛物线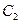 :
: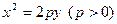 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线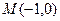 的直线
的直线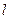 与抛物线
与抛物线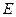 、
、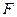 两点,又过
两点,又过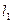 、
、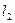 ,当
,当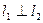 时,求直线
时,求直线