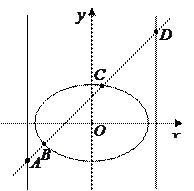题目内容
(本小题满分13分)若椭圆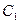 :
: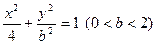 的离心率等于
的离心率等于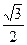 ,抛物线
,抛物线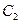 :
: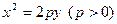 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线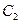 的方程;
的方程;
(Ⅱ)求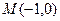 的直线
的直线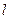 与抛物线
与抛物线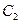 交
交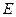 、
、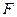 两点,又过
两点,又过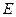 、
、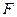 作抛物线
作抛物线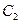 的切线
的切线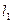 、
、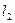 ,当
,当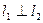 时,求直线
时,求直线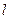 的方程;
的方程;
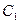 :
: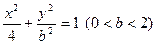 的离心率等于
的离心率等于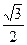 ,抛物线
,抛物线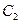 :
: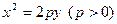 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线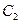 的方程;
的方程;(Ⅱ)求
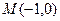 的直线
的直线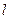 与抛物线
与抛物线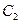 交
交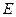 、
、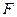 两点,又过
两点,又过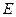 、
、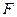 作抛物线
作抛物线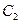 的切线
的切线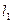 、
、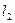 ,当
,当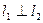 时,求直线
时,求直线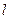 的方程;
的方程;(Ⅰ) 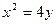 (Ⅱ)
(Ⅱ) 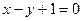
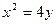 (Ⅱ)
(Ⅱ) 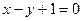
(I)已知椭圆的长半轴为2,半焦距
由离心率等于 ……2分
……2分
 ………3分
………3分
 椭圆的上顶点(0,1)
椭圆的上顶点(0,1)  抛物线的焦点为(0,1)
抛物线的焦点为(0,1) 抛物线的方程为
抛物线的方程为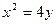
(II)由已知,直线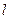 的斜率必存在,设直线
的斜率必存在,设直线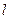 的方程为
的方程为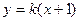 ,
,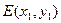 ,
, ,
,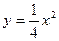 ,
,
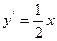 ,
, 切线
切线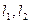 的斜率分别为
的斜率分别为 …………8分
…………8分
当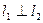 时,
时,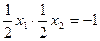 ,即
,即 ………………………………9分
………………………………9分
由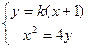 得:
得:
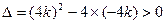 解得
解得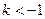 或
或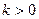 ①
①

 ,即:
,即: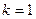 ……12分
……12分
此时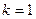 满足①
满足①  直线
直线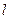 的方程为
的方程为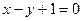 …………13分
…………13分

由离心率等于
 ……2分
……2分
 ………3分
………3分 椭圆的上顶点(0,1)
椭圆的上顶点(0,1)  抛物线的焦点为(0,1)
抛物线的焦点为(0,1) 抛物线的方程为
抛物线的方程为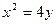
(II)由已知,直线
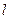 的斜率必存在,设直线
的斜率必存在,设直线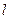 的方程为
的方程为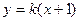 ,
,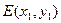 ,
, ,
,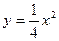 ,
,
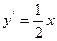 ,
, 切线
切线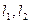 的斜率分别为
的斜率分别为 …………8分
…………8分当
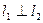 时,
时,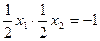 ,即
,即 ………………………………9分
………………………………9分由
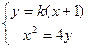 得:
得:
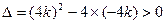 解得
解得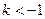 或
或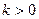 ①
①
 ,即:
,即: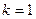 ……12分
……12分此时
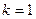 满足①
满足①  直线
直线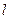 的方程为
的方程为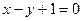 …………13分
…………13分
练习册系列答案
相关题目
 过定点
过定点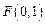 ,且和定直线
,且和定直线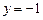 相切.(Ⅰ)求动圆圆心
相切.(Ⅰ)求动圆圆心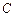 的方程;(Ⅱ)已知点
的方程;(Ⅱ)已知点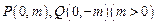 ,过点
,过点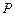 作直线与曲线
作直线与曲线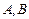 两点,若
两点,若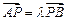 (
(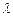
 为实数),证明:
为实数),证明: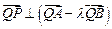 .
.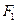 与抛物线
与抛物线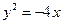 的焦点重合,过
的焦点重合,过 与椭圆交于A、B两点,与抛物线交于C、D两点.当直线
与椭圆交于A、B两点,与抛物线交于C、D两点.当直线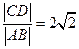 .
.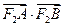 的最大值和最小值.
的最大值和最小值.
 :
: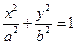
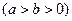 的两个焦点为
的两个焦点为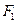 、
、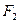 ,点
,点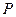 在椭圆
在椭圆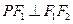 ,
,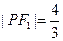 ,
,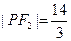 .
. 过圆
过圆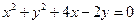 的圆心
的圆心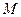 ,交椭圆
,交椭圆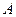 、
、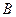 两点,且
两点,且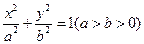 的离心率
的离心率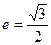 ,过A(a,0),
,过A(a,0),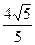 .
. 0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值. 和椭圆
和椭圆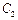 有相同的焦点
有相同的焦点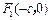 和
和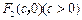 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为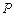 ,椭圆
,椭圆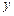 轴负半轴交于点
轴负半轴交于点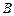 ,且
,且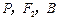 三点共线,
三点共线,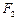 分有向线段
分有向线段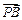 的比为
的比为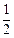 ,又直线
,又直线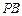 与双曲线
与双曲线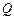 ,若
,若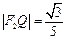 .
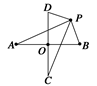
.



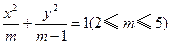 ,过其左焦点且斜率为
,过其左焦点且斜率为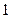 的直线与椭圆及其准线的交点从左到右的顺序为
的直线与椭圆及其准线的交点从左到右的顺序为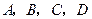 (如图),设
(如图),设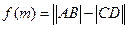 .
.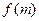 的解析式;
的解析式;