题目内容
函数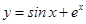 的图象上一点(0,1)处的切线的斜率为( )
的图象上一点(0,1)处的切线的斜率为( )
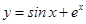 的图象上一点(0,1)处的切线的斜率为( )
的图象上一点(0,1)处的切线的斜率为( )| A.1 | B.2 | C.3 | D.0 |
B
试题分析:因为函数
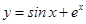 的导数为
的导数为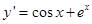 ,所以
,所以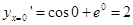 .即函数
.即函数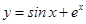 的图象上一点(0,1)处的切线的斜率为2,故选B.本校题关键是考查导数的几何意义,以及三角函数的导数.
的图象上一点(0,1)处的切线的斜率为2,故选B.本校题关键是考查导数的几何意义,以及三角函数的导数.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
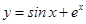 的图象上一点(0,1)处的切线的斜率为( )
的图象上一点(0,1)处的切线的斜率为( )| A.1 | B.2 | C.3 | D.0 |
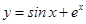 的导数为
的导数为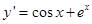 ,所以
,所以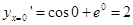 .即函数
.即函数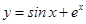 的图象上一点(0,1)处的切线的斜率为2,故选B.本校题关键是考查导数的几何意义,以及三角函数的导数.
的图象上一点(0,1)处的切线的斜率为2,故选B.本校题关键是考查导数的几何意义,以及三角函数的导数.
 阅读快车系列答案
阅读快车系列答案