Question

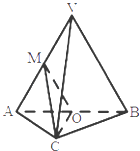
【题目】如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C．

（1）证明：B1C⊥AB；
（2）若AC⊥AB1 ， ∠CBB1=60°，BC=2，求B1到平面ABC的距离．

Answer 1

【答案】
（1）证明：连结BC1，则BC1与B1C交于O，

∵侧面BB1C1C为菱形，∴B1C⊥BC1，

∵AO⊥平面BB1C1C，∴B1C⊥AO

又∵BC1∩AO=O，

∴B1C⊥平面ABO，

由于AB平面ABO，∴B1C⊥AB

（2）解：设点B1 到平面ABC 的距离为h，

∵侧面BB1C1C为菱形，∠CBB1=60°，BC=2，

∴△CBB1为等边三角形，

∴BC=BB1=B1C=2，BO=

∵AC⊥AB1，∴ ，

Rt△AOB中，AB= =2

∴S△ABC= = ，

∵ = ，

∴ ，

∴h= ．

∴点B1 到平面ABC 的距离为

【解析】（1）要证B1C⊥AB，即证B1C⊥平面ABC1 ， 由菱形的对角线垂直和线面垂直的性质，即可得证；（2）由棱锥的体积公式，利用 = ，即可得到B1到平面ABC的距离．