题目内容
【题目】如图,在三棱锥V﹣ABC中,平面VA B⊥平面 ABC,AC=BC,O,M分别为A B,VA的中点. 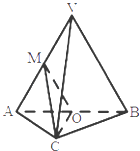
(1)求证:VB∥平面 M OC;
(2)求证:平面MOC⊥平面VAB.
【答案】
(1)证明:∵M,O分别为VA,AB的中点,
∴MO∥VB,又MO面MOC,VB面MOC,
∴VB∥面MOC.
(2)∵AC=BC,O为AB的中点,
∴OC⊥AB.又∵平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,OC平面ABC,
∴OC⊥平面VAB.又∵OC平面MOC,
∴平面MOC⊥平面VAB.
【解析】(1)利用中位线定理可得MO∥VB,从而得出VB∥平面MOC;(2)由三线合一可得OC⊥AB,由平面VAB⊥平面ABC可得OC⊥平面VAB,故而平面MOC⊥平面VAB.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目
【题目】给出最小二乘法下的回归直线方程 ![]() =
= ![]() x+
x+ ![]() 系数公式:
系数公式: ![]() =
= 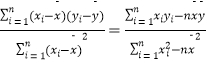 ,
, ![]()
假设关于某设备的使用年限x(年)和所支出的维修费用y(万元),有如表的统计资料:
使用年限x (年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为12年时,维修费用是多少?