题目内容
【题目】已知圆C过点M(0,﹣2),N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)问是否存在满足以下两个条件的直线l:①斜率为1;②直线被圆C截得的弦为AB,以AB为直径的圆C1过原点.若存在这样的直线,请求出其方程;若不存在,说明理由.
【答案】
(1)解:设圆C的方程为x2+y2+Dx+Ey+F=0
则 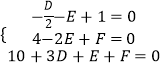 解得D=﹣6,E=4,F=4
解得D=﹣6,E=4,F=4
∴圆C方程为x2+y2﹣6x+4y+4=0
(2)解:设直线存在,其方程为y=x+b,它与圆C的交点设为A(x1,y1)、B(x2,y2),
则由 ![]() 得2x2+2(b﹣1)x+b2+4b+4=0(*)
得2x2+2(b﹣1)x+b2+4b+4=0(*)
∴ 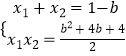
∴y1y2=(x1+b)(x2+b)= ![]() ,
,
∵AB为直径,∴,∠AOB=90°,∴OA2+OB2=AB2,
∴ ![]()
得x1x2+y1y2=0,
∴ ![]() ,
,
即b2+4b+4+b(1﹣b)+b2=0,b2+5b+4=0,∴b=﹣1或b=﹣4
容易验证b=﹣1或b=﹣4时方程(*)有实根.
故存在这样的直线l有两条,其方程是y=x﹣1或y=x﹣4.
【解析】(1)设圆C的方程为x2+y2+Dx+Ey+F=0,利用点在圆上,圆心在直线上,列出方程组,解得D,E,F,即可求得圆C方程.(2)设直线存在,其方程为y=x+b,它与圆C的交点设为A(x1 , y1)、B(x2 , y2),利用直线与圆的方程联立方程组,利用韦达定理,推出x1x2 , y1y2 , 利用垂直关系得到 ![]() ,求得b=﹣1或b=﹣4时方程(*)有实根.说明存在这样的直线l有两条,即可.
,求得b=﹣1或b=﹣4时方程(*)有实根.说明存在这样的直线l有两条,即可.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目