题目内容
已知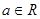 ,函数
,函数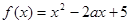 .
.
⑴若不等式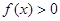 对任意
对任意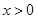 恒成立,求实数
恒成立,求实数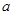 的最值范围;
的最值范围;
⑵若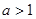 ,且函数
,且函数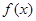 的定义域和值域均为
的定义域和值域均为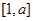 ,求实数
,求实数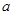 的值.
的值.
(1)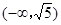 ;(2)
;(2)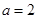 .
.
解析试题分析:(1)根据题意,若不等式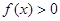 对任意
对任意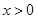 恒成立,参编分离后即可得:
恒成立,参编分离后即可得: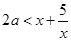 ,从而问题等价于求使
,从而问题等价于求使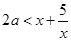 对于任意
对于任意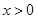 恒成立的
恒成立的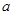 的范围,而
的范围,而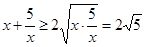 ,当且仅当
,当且仅当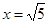 时,“=”成立,故实数
时,“=”成立,故实数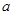 的取值范围是
的取值范围是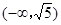 ;(2)由题意可得
;(2)由题意可得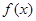 为二次函数,其对称轴为
为二次函数,其对称轴为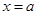 ,因此当
,因此当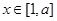 时,可得其值域应为
时,可得其值域应为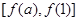 ,从而结合条件
,从而结合条件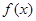 的定义域和值域都是
的定义域和值域都是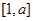 可得关于
可得关于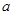 的方程组
的方程组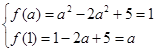 ,即可解得
,即可解得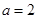 .
.
试题解析:(1)∵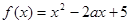 ,∴
,∴ 可变形为:
可变形为: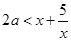 ,而
,而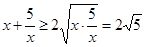 ,当且仅当
,当且仅当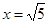 时,“=”成立,∴要使不等式
时,“=”成立,∴要使不等式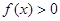 对任意
对任意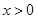 恒成立,只需
恒成立,只需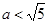 ,即实数
,即实数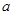 的取值范围是
的取值范围是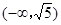 ;
;
(2)∵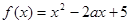 ,∴其图像对称轴为
,∴其图像对称轴为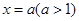 ,根据二次函数的图像,可知
,根据二次函数的图像,可知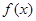 在
在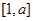 上单调递减,∴当
上单调递减,∴当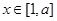 时,其值域为
时,其值域为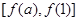 ,又由
,又由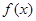 的值域是
的值域是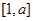 ,
,
∴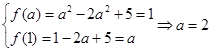 .
.
考点:1.恒成立问题的处理方法;2.二次函数的值域.

练习册系列答案
相关题目
 (sinx+cosx); ④f(x)=
(sinx+cosx); ④f(x)= ;
; ),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性.
),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性. 上恒有f(x)
上恒有f(x)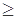 -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围. 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 ;
; 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于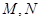 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
. 表示为
表示为 的函数;
的函数; 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.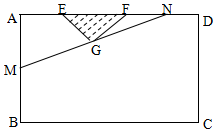
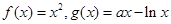 ,
,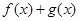 在
在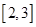 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;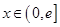 (
(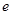 是自然常数)时,函数
是自然常数)时,函数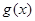 的最小值是3,若存在,求出
的最小值是3,若存在,求出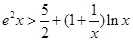 .
.