题目内容
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于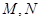 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.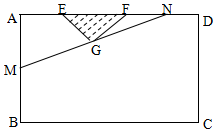
(1)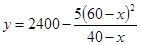 ;(2)当
;(2)当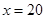 时,到的市民健身广场面积最大,最大面积为
时,到的市民健身广场面积最大,最大面积为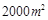 .
.
解析试题分析:(1)根据题意分析可考虑作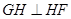 ,垂足为
,垂足为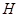 ,从而可将五边形的面积转化为梯形
,从而可将五边形的面积转化为梯形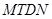 与矩形
与矩形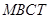 的面积之和,由
的面积之和,由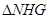 ∽
∽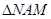 结合条件,可将梯形
结合条件,可将梯形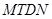 的上底,下底与高以及矩形
的上底,下底与高以及矩形 的长和宽都用含
的长和宽都用含 的代数式表示出来,从而可得:
的代数式表示出来,从而可得: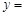
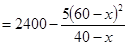 ,再由
,再由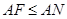 ,可得
,可得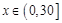 ;(2)由(1)及条件可知,问题就等价于求函数
;(2)由(1)及条件可知,问题就等价于求函数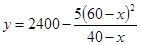 在
在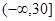 上的最大值,而将其变形后可得:
上的最大值,而将其变形后可得: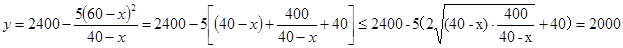 ,
,
当且仅当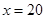 时,“=”成立,从而当
时,“=”成立,从而当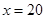 时,到的市民健身广场面积最大,最大面积为
时,到的市民健身广场面积最大,最大面积为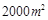 .
.
试题解析:(1)如图,作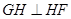 ,垂足为
,垂足为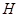 ,
,
∵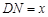 ,∴
,∴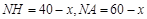 ,又由
,又由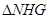 ∽
∽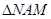 ,∴
,∴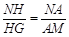 ,
,
∵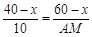 ,∴
,∴ , 2分
, 2分
过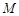 作
作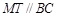 交
交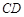 于
于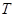 ,
,
则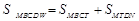
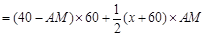 ,
,
所以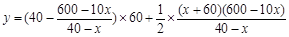
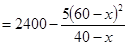 , 7分
, 7分
由于 与
与 重合时,
重合时,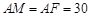 适合条件,故
适合条件,故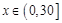 ; 8分
; 8分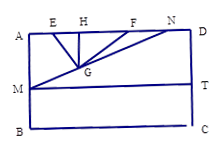
(2)由(1)得: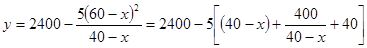 , 10分
, 10分
∴当且仅当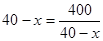 ,即
,即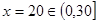 时,
时,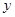 取得最大值
取得最大值 , 13分
, 13分
即当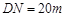 时,得到的市民健身广场面积最大,最大面积为
时,得到的市民健身广场面积最大,最大面积为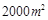 . 14分
. 14分
考点:1.函数的运用;2.基本不等式求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
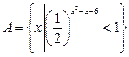 ,
,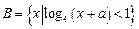 ,若
,若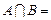
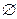 ,则实数a
,则实数a 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m, ;
; 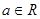 ,函数
,函数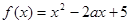 .
.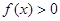 对任意
对任意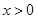 恒成立,求实数
恒成立,求实数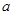 的最值范围;
的最值范围;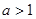 ,且函数
,且函数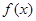 的定义域和值域均为
的定义域和值域均为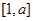 ,求实数
,求实数 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量 的二次项系数为
的二次项系数为 ,且不等式
,且不等式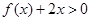 的解集为(1,3).
的解集为(1,3). 有两个相等实数根,求
有两个相等实数根,求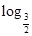
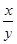 的值.
的值.