题目内容
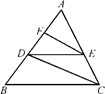
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP // AC,交AB于点E,交圆O在A点处的切线于点P.求证:△PAE∽△BDE.


详见解析
试题分析:根据圆的性质:弦切角等于劣弧所对的圆周角,即可得∠PAB=∠ACB,又由对顶角相等即可得两三角形中两角相等,即可得证.
试题解析:因为PA是圆O在点A处的切线,所以∠PAB=∠ACB.
因为PD∥AC,所以∠EDB=∠ACB,
所以∠PAE=∠PAB=∠ACB=∠BDE.
又∠PEA=∠BED,故△PAE∽△BDE. 10分

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
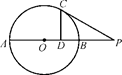
 的直径
的直径 ,
, 为圆周上一点,
为圆周上一点, ,过
,过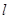 ,则点
,则点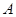 到直线
到直线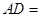 ___________.
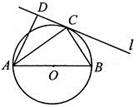
___________.

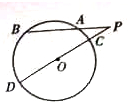
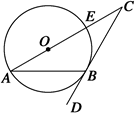
 的弦ED,CB的延长线交于点A,若BD
的弦ED,CB的延长线交于点A,若BD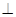 AE,AB=4,BC=2,AD=3,则CE= ;
AE,AB=4,BC=2,AD=3,则CE= ; 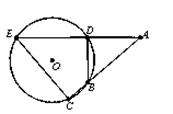
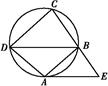
 是半圆周上的两个三等分点,直径
是半圆周上的两个三等分点,直径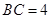 ,
,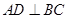 ,垂足为D,
,垂足为D, 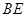 与
与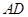 相交与点F,则
相交与点F,则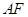 的长为 。
的长为 。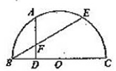
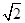 ,求AF的长.
,求AF的长.