Question

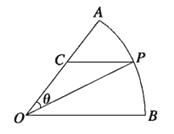
【题目】已知：如图，两同心圆： 和. 为大圆上一动点，连结（为坐标原点）交小圆于点，过点作轴垂线（垂足为），再过点作直线的垂线，垂足为.

（1）当点在大圆上运动时，求垂足的轨迹方程；

（2）过点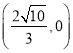的直线交垂足的轨迹于两点，若以为直径的圆与轴相切，求直线的方程.

Answer 1

【答案】（1）；（2）直线的方程为： .

【解析】试题分析：（1）设垂足，则，将点P坐标代入圆方程可得点Q的方程。（2）设的方程为， ，则由弦长公式，又由圆与轴相切得，将直线方程代入椭圆方程消元后得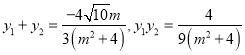，根据以上各式可解得，可求得直线方程。

试题解析：

（1）设垂足，则

因为在上，

所以，

所以

故垂足的轨迹方程为

（2）设直线的方程为，

则有，

又因为圆与轴相切，

所以

即（*）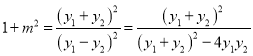

由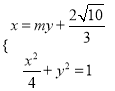消去x整理得，

因为直线与椭圆交于两点，

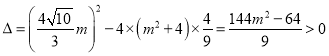所以，解得。

又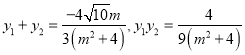

将上式代入（*）式中得，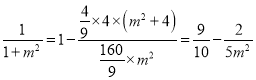

解得。满足。

故所求的直线的方程为，

即