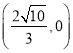题目内容
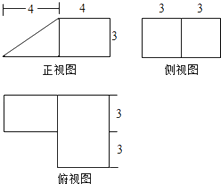
【题目】将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内，使得正方体能够任意自由地转动，则a的最大值为 ．
【答案】
【解析】解：若在四个半径为1且两两相切的实心小球所形成的球间空隙内放置一个与其它球都相切的小球，
设该小球的半径为r，
则r+1+ 
= 
，
解得：r= 
，
若将一个棱长为a的正方体嵌入到四个半径为1且两两相切的实心小球所形成的球间空隙内，使得正方体能够任意自由地转动，
则： 
a=2r，
解得：a= ，
所以答案是： ．
【考点精析】根据题目的已知条件，利用球内接多面体的相关知识可以得到问题的答案，需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．
练习册系列答案
相关题目
【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数
（份）与收入
（元）之间有如下的对应数据：
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
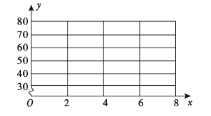
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：①参考公式：线性回归方程系数公式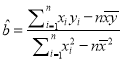
， 
；
②参考数据： 
， 
， 
．
