题目内容
【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处有公共切线,求a,b的值;
(2)当a=3,b=﹣9时,函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
【答案】
(1)解:f(x)=ax2+1(a>0),则f′(x)=2ax,k1=2a,
g(x)=x3+bx,则g′(x)=3x2+b,k2=3+b,
由(1,c)为公共切点,可得:2a=3+b ①
又f(1)=a+1,g(1)=1+b,
∴a+1=1+b,
即a=b,代入①式,可得:a=3,b=3.
(2)解:当a=3,b=﹣9时,设h(x)=f(x)+g(x)=x3+3x2﹣9x+1
则h′(x)=3x2+6x﹣9,
令h'(x)=0,
解得:x1=﹣3,x2=1;
∴k≤﹣3时,函数h(x)在(﹣∞,﹣3)上单调增,在(﹣3,1]上单调减,(1,2)上单调增,所以在区间[k,2]上的最大值为h(﹣3)=28
﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28
所以k的取值范围是(﹣∞,﹣3]
【解析】(1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;(2)当a=3,b=﹣9时,设h(x)=f(x)+g(x)=x3+3x2﹣9x+1,求导函数,确定函数的极值点,进而可得k≤﹣3时,函数h(x)在区间[k,2]上的最大值为h(﹣3)=28;﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28,由此可得结论.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
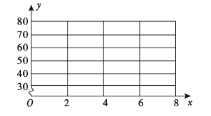
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式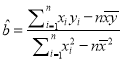 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.