题目内容
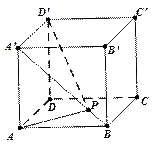
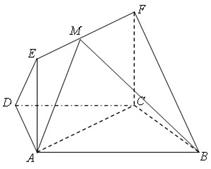
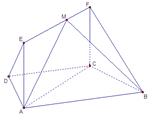
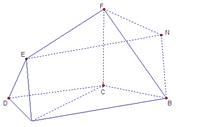
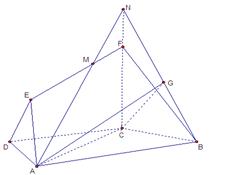
((本小题12分)如图,在梯形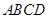 中,
中,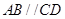 ,
,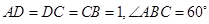 ,四边形
,四边形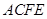 为矩形,平面
为矩形,平面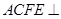 平面
平面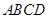 ,
,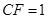 .
.
(1)求证: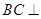 平面
平面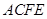 ;
;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点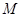 在线段
在线段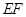 上运动,设平面
上运动,设平面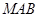 与平面
与平面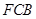 所成二面角的平面角为
所成二面角的平面角为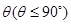 ,试求
,试求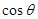 的取值范围.
的取值范围.
 中,
中,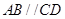 ,
,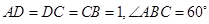 ,四边形
,四边形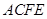 为矩形,平面
为矩形,平面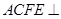 平面
平面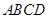 ,
,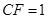 .
.(1)求证:
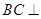 平面
平面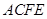 ;
;(2)求二面角A-BF-C的平面角的余弦值;
(3)若点
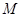 在线段
在线段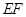 上运动,设平面
上运动,设平面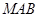 与平面
与平面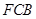 所成二面角的平面角为
所成二面角的平面角为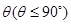 ,试求
,试求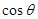 的取值范围.
的取值范围.
(1)证明:在梯形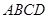 中, ∵
中, ∵ 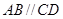 ,
,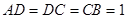 ,
,
∠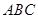 =
=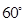 ,∴
,∴ 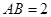 ∴
∴ 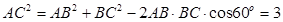
∴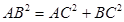 ∴
∴ 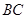 ⊥
⊥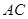
∵平面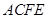 ⊥平面
⊥平面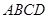 ,
,
平面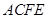 ∩平面
∩平面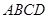
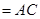 ,
,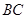
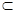 平面
平面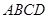
∴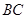 ⊥平面
⊥平面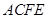
(2)取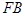 中点为
中点为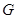 ,连结
,连结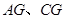
∵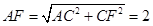 ,∴
,∴ 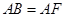 ∴
∴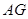 ⊥
⊥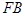 ∵
∵ 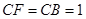 ∴
∴  ⊥
⊥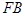 ∴ ∠
∴ ∠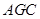 =
=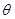
∵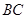
 ⊥
⊥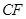 ∴
∴ 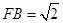 ∴
∴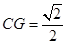 ,
,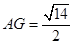
∴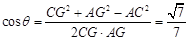
(3)由(2)知,①当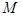 与
与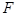 重合时,
重合时,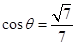
②当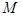 与
与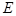 重合时,过
重合时,过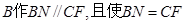 ,连结
,连结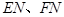 ,则平面
,则平面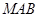 ∩平面
∩平面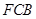 =
=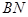 ,∵
,∵ 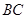 ⊥
⊥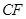 ,又∵
,又∵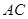 ⊥
⊥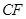 ∴
∴ 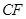 ⊥平面
⊥平面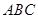 ∴
∴ 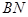 ⊥平面
⊥平面
∴ ∠ =
=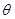 ∴
∴ 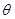 =
=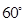 ,∴
,∴ 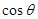 =
=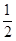
③当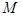 与
与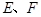 都不重合时,令
都不重合时,令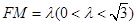
延长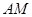 交
交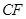 的延长线于
的延长线于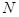 ,连结
,连结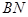
∴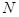 在平面
在平面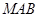 与平面
与平面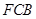 的交线上
的交线上
∵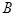 在平面
在平面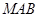 与平面
与平面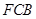 的交线上
的交线上
∴ 平面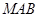 ∩平面
∩平面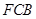 =
=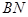
过C作CH⊥NB交NB于H ,连结AH,
由(I)知,
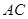 ⊥
⊥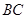 , 又∵AC⊥CN,∴ AC⊥平面NCB
, 又∵AC⊥CN,∴ AC⊥平面NCB
∴ AC⊥NB, 又∵ CH⊥NB,AC∩CH=C,∴ NB⊥平面ACH ∴AH⊥NB ∴ ∠AHC=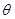
在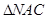 中,可求得NC=
中,可求得NC=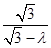 ,从而,在
,从而,在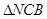 中,可求得CH=
中,可求得CH=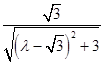
∵ ∠ACH=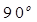 ∴ AH=
∴ AH=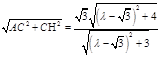
∴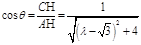 ∵
∵ 
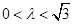 ∴
∴ 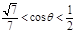 , 综上得
, 综上得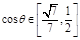 。
。
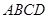 中, ∵
中, ∵ 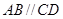 ,
,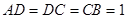 ,
,∠
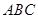 =
=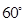 ,∴
,∴ 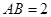 ∴
∴ 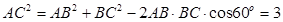
∴
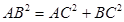 ∴
∴ 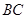 ⊥
⊥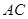
∵平面
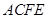 ⊥平面
⊥平面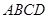 ,
,平面
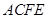 ∩平面
∩平面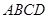
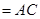 ,
,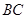
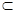 平面
平面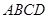
∴
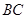 ⊥平面
⊥平面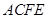
(2)取
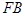 中点为
中点为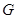 ,连结
,连结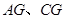
∵
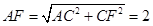 ,∴
,∴ 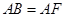 ∴
∴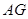 ⊥
⊥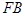 ∵
∵ 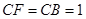 ∴
∴  ⊥
⊥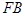 ∴ ∠
∴ ∠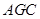 =
=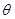

∵
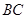
 ⊥
⊥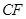 ∴
∴ 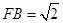 ∴
∴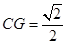 ,
,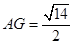
∴
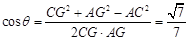

(3)由(2)知,①当
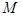 与
与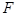 重合时,
重合时,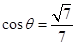
②当
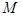 与
与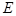 重合时,过
重合时,过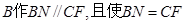 ,连结
,连结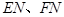 ,则平面
,则平面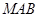 ∩平面
∩平面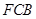 =
=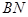 ,∵
,∵ 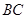 ⊥
⊥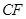 ,又∵
,又∵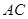 ⊥
⊥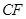 ∴
∴ 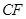 ⊥平面
⊥平面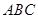 ∴
∴ 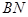 ⊥平面
⊥平面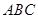

∴ ∠
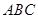 =
=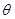 ∴
∴ 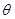 =
=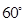 ,∴
,∴ 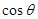 =
=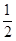
③当
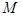 与
与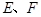 都不重合时,令
都不重合时,令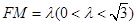
延长
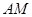 交
交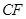 的延长线于
的延长线于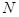 ,连结
,连结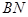
∴
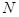 在平面
在平面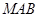 与平面
与平面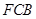 的交线上
的交线上∵
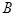 在平面
在平面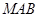 与平面
与平面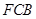 的交线上
的交线上∴ 平面
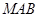 ∩平面
∩平面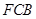 =
=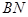
过C作CH⊥NB交NB于H ,连结AH,
由(I)知,

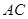 ⊥
⊥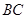 , 又∵AC⊥CN,∴ AC⊥平面NCB
, 又∵AC⊥CN,∴ AC⊥平面NCB∴ AC⊥NB, 又∵ CH⊥NB,AC∩CH=C,∴ NB⊥平面ACH ∴AH⊥NB ∴ ∠AHC=
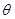
在
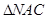 中,可求得NC=
中,可求得NC=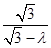 ,从而,在
,从而,在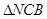 中,可求得CH=
中,可求得CH=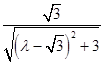
∵ ∠ACH=
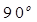 ∴ AH=
∴ AH=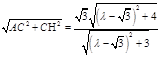
∴
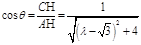 ∵
∵ 
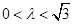 ∴
∴ 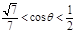 , 综上得
, 综上得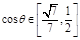 。
。略

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
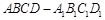 中,
中,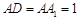 ,
,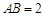 ,当E为AB中点时,求二面角
,当E为AB中点时,求二面角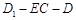 的余弦值.
的余弦值.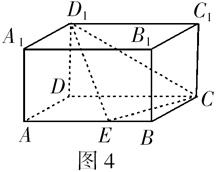

 的大小。
的大小。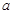 与平面
与平面 没有公共点,则
没有公共点,则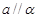 ;
; ,则
,则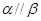
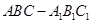 中的每一个顶点都在同一个球面上,如果
中的每一个顶点都在同一个球面上,如果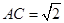 ,
,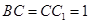 ,
,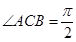 ,那么
,那么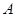 、
、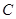 两点间的球面距离是
两点间的球面距离是  若CM=BN=a(0<a<
若CM=BN=a(0<a<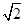 ).
).
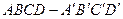 的面对角线
的面对角线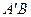 上存在一点
上存在一点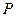 使得
使得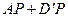 取得最小值,则此最小值为
取得最小值,则此最小值为