题目内容
在数列{an}中,a1=1,且Sn,Sn+1,2S1成等差数列(Sn表示数列{an}的前n项和),则S2,S3,S4分别为__________________,猜想Sn=________.
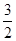 ,
,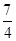 ,
,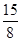
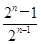
由Sn,Sn+1,2S1成等差数列,得2Sn+1=Sn+2S1,
因为S1=a1=1,所以2Sn+1=Sn+2.
令n=1,则2S2=S1+2=1+2=3⇒S2=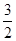 ,
,
同理,分别令n=2,n=3,可求得S3=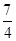 ,S4=
,S4=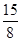 .
.
由S1=1=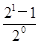 ,S2=
,S2=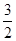 =
=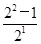 ,
,
S3=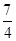 =
=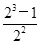 ,S4=
,S4=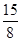 =
=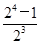 ,猜想Sn=
,猜想Sn=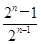 .
.
因为S1=a1=1,所以2Sn+1=Sn+2.
令n=1,则2S2=S1+2=1+2=3⇒S2=
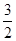 ,
,同理,分别令n=2,n=3,可求得S3=
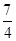 ,S4=
,S4=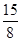 .
.由S1=1=
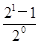 ,S2=
,S2=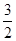 =
=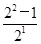 ,
,S3=
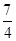 =
=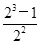 ,S4=
,S4=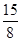 =
=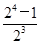 ,猜想Sn=
,猜想Sn=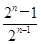 .
.
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
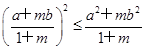 .
.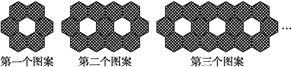
 .设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
.设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥 ,如果用
,如果用 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么类比得到的结论是 .
表示截面面积,那么类比得到的结论是 .
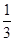 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
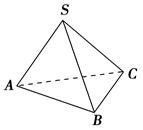
 a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= . 则ak+1=( ).
则ak+1=( ).
 -
-