题目内容
在平面几何里可以得出正确结论:“正三角形的内切圆半径等于这正三角形的高的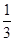 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
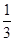 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .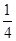
运用分割法思想,设正四面体的高为h,底面面积为S,正四面体SABC的内切球的半径为R,球心为O,连结OS、OA、OB、OC,将四面体分成四个三棱锥,则VS ABC=VO SAC+VO SAB+VO SBC+VO ABC=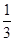 SR+
SR+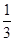 SR+
SR+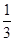 SR+
SR+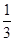 SR=
SR=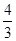 SR=
SR=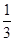 Sh,所以R=
Sh,所以R=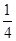 h.
h.
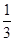 SR+
SR+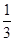 SR+
SR+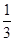 SR+
SR+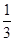 SR=
SR=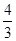 SR=
SR=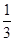 Sh,所以R=
Sh,所以R=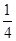 h.
h.
练习册系列答案
相关题目
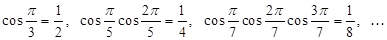 ,根据这些结果,猜想
,根据这些结果,猜想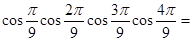
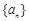 的前
的前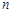 项和为
项和为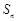 ,且
,且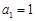 ,
,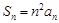
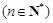 ,可归纳猜想出
,可归纳猜想出



 +2=4;
+2=4; +3=
+3= ;
; +4=
+4= ;
;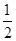 ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为________________,由此猜想an=________.
,则a2,a3,a4,a5的值分别为________________,由此猜想an=________. ,f(1)=1(x∈N*),猜想f(x)的表达式为( )
,f(1)=1(x∈N*),猜想f(x)的表达式为( )


