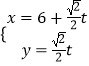ЬтФПФкШн
ЁОЬтФПЁПеФжнЫЎЯЩСлОЅЫЖДѓЃЌМ§ЖрЛЈЗБЃЌЩЋУРЯугєЃЌЫибХОъРіЃЌгаЁАЬьЯТЫЎЯЩЪ§еФжнЁБжЎУРгўЃЎЯжФГЫЎЯЩЛЈЕёПЬЪІЪмЙЭУПЬьЕёПЬ250СЃЫЎЯЩЛЈЃЌЕёПЬЪІУПЕёПЬвЛСЃПЩзЌ1.2дЊЃЌШчЙћЕёПЬЪІЕБЬьГЌЖюЭъГЩШЮЮёЃЌдђГЌГіЕФВПЗжУПСЃзЌ1.7дЊЃЛШчЙћЕБЬьЮДФмАДСПЭъГЩШЮЮёЃЌдђАДЪЕМЪЭъГЩЕФЕёПЬСПСьШЁЕБЬьЙЄзЪЃЎ ЃЈIЃЉЧѓЕёПЬЪІЕБЬьЪеШыЃЈЕЅЮЛЃКдЊЃЉЙигкЕёПЬСПnЃЈЕЅЮЛЃКСЃЃЌnЁЪNЃЉЕФКЏЪ§НтЮіЪНfЃЈnЃЉЃЛ
ЃЈЂђЃЉИУЕёПЬЪІМЧТМСЫЙ§ШЅ10ЬьУПЬьЕФЕёПЬСПnЃЈЕЅЮЛЃКСЃЃЉЃЌећРэЕУШчБэЃК
ЕёПЬСПn | 210 | 230 | 250 | 270 | 300 |
ЦЕЪ§ | 1 | 2 | 3 | 3 | 1 |
вд10ЬьМЧТМЕФИїЕёПЬСПЕФЦЕТЪзїЮЊИїЕёПЬСПЗЂЩњЕФИХТЪЃЎ
ЃЈЂЁЃЉЧѓИУЕёПЬЪІет10ЬьЕФЦНОљЪеШыЃЛ
ЃЈЂЂЃЉЧѓИУЕёПЬЪІЕБЬьЪеШыВЛЕЭгк300дЊЕФИХТЪЃЎ
ЁОД№АИЁПНтЃКЃЈЂёЃЉЕБnЁн250ЪБЃЌfЃЈnЃЉ=250ЁС1.2+1.7ЁСЃЈnЉ250ЃЉ=1.7nЉ125ЃЌ
ЕБnЃМ250ЪБЃЌfЃЈnЃЉ=1.2nЃЌ
ЁрЕёПЬЪІЕБЬьЪеШыЃЈЕЅЮЛЃКдЊЃЉЙигкЕёПЬСПnЃЈЕЅЮЛЃКСЃЃЌnЁЪNЃЉЕФКЏЪ§НтЮіЪНЃК
fЃЈnЃЉ= ![]() ЃЌЃЈnЁЪNЃЉЃЎ
ЃЌЃЈnЁЪNЃЉЃЎ
ЃЈЂђЃЉЃЈiЃЉгЩЬтвтЕУfЃЈ210ЃЉ=252ЃЌfЃЈ230ЃЉ=276ЃЌfЃЈ250ЃЉ=300ЃЌfЃЈ270ЃЉ=334ЃЌfЃЈ300ЃЉ=385ЃЌ
ЁрXЕФПЩФмШЁжЕЮЊ252ЃЌ276ЃЌ300ЃЌ334ЃЌ385ЃЌ
PЃЈX=252ЃЉ=0.1ЃЌPЃЈX=276ЃЉ=0.2ЃЌPЃЈX=300ЃЉ=0.3ЃЌ
PЃЈX=334ЃЉ=0.3ЃЌPЃЈX=385ЃЉ=0.1ЃЌ
ЁрXЕФЗжВМСаЮЊЃК
X | 252 | 276 | 300 | 334 | 385 |
P | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
EЃЈXЃЉ=252ЁС0.1+276ЁС0.2+300ЁС0.3+334ЁС0.3+385ЁС0.1=338ЃЈдЊЃЉЃЌ
ЁрИУЕёПЬЪІет10ЬьЕФЦНОљЪеШыЮЊ338дЊЃЎ
ЃЈiiЃЉгЩXЕФЗжВМСажЊЃК
ИУЕёПЬЪІЕБЬьЪеШыВЛЕЭгк300дЊЕФИХТЪЃК
P=PЃЈX=300ЃЉ+PЃЈX=334ЃЉ+PЃЈX=385ЃЉ
=0.3+0.3+0.1=0.7
ЁОНтЮіЁПЃЈЂёЃЉЕБnЁн250ЪБЃЌfЃЈnЃЉ=250ЁС1.2+1.7ЁСЃЈnЉ250ЃЉЃЌЕБnЃМ250ЪБЃЌfЃЈnЃЉ=1.2nЃЌгЩДЫФмЧѓГіЕёПЬЪІЕБЬьЪеШыЃЈЕЅЮЛЃКдЊЃЉЙигкЕёПЬСПnЃЈЕЅЮЛЃКСЃЃЌnЁЪNЃЉЕФКЏЪ§НтЮіЪНЃЎЃЈЂђЃЉЃЈiЃЉгЩЬтвтЕУfЃЈ210ЃЉ=252ЃЌfЃЈ230ЃЉ=276ЃЌfЃЈ250ЃЉ=300ЃЌfЃЈ270ЃЉ=334ЃЌfЃЈ300ЃЉ=385ЃЌXЕФПЩФмШЁжЕЮЊ252ЃЌ276ЃЌ300ЃЌ334ЃЌ385ЃЌЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫФмЧѓГіИУЕёПЬЪІет10ЬьЕФЦНОљЪеШыЃЎЃЈiiЃЉгЩXЕФЗжВМСажЊИУЕёПЬЪІЕБЬьЪеШыВЛЕЭгк300дЊЕФИХТЪЃКP=PЃЈX=300ЃЉ+PЃЈX=334ЃЉ+PЃЈX=385ЃЉЃЌгЩДЫФмЧѓГіНсЙћЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГЙЋЫОЮЊЦРЙРСНЬзДйЯњЛюЖЏЗНАИЃЈЗНАИ1дЫзїЗбгУЮЊ5дЊ/МўЃЛЗНАИ2ЕФдЫзїЗбгУЮЊ2дЊ/МўЃЉЃЌдкФГЕиЧјВПЗжгЊЯњЭјЕуНјааЪдЕуЃЈУПИіЪдЕуЭјЕужЛВЩгУвЛжжДйЯњЛюЖЏЗНАИЃЉЃЌдЫзївЛФъКѓЃЌЖдБШИУЕиЧјЩЯвЛФъЖШЕФЯњЪлЧщПіЃЌжЦзїЯргІЕФЕШИпЬѕаЮЭМШчЭМЫљЪОЃЎ 
ЃЈ1ЃЉЧыИљОнЕШИпЬѕаЮЭМЬсЙЉЕФаХЯЂЃЌЮЊИУЙЋЫОНёФъбЁдёвЛЬзНЯЮЊгаРћЕФДйЯњЛюЖЏЗНАИЃЈВЛБиЫЕУїРэгЩЃЉЃЛ
ЃЈ2ЃЉвбжЊИУЙЋЫОВњЦЗЕФГЩБОЮЊ10дЊ/МўЃЈЮДАќРЈДйЯњЛюЖЏдЫзїЗбгУЃЉЃЌЮЊжЦЖЈБОФъЖШИУЕиЧјЕФВњЦЗЯњЪлМлИёЃЌЭГМЦЩЯвЛФъЖШЕФ8зщЪлМлxiЃЈЕЅЮЛЃКдЊ/МўЃЌећЪ§ЃЉКЭЯњСПyiЃЈЕЅЮЛЃКМўЃЉЃЈi=1ЃЌ2ЃЌЁЃЌ8ЃЉШчЯТБэЫљЪОЃК
ЪлМлx | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
ЯњСПy | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
ЂйЧыИљОнЯТСаЪ§ОнМЦЫуЯргІЕФЯрЙижИЪ§R2 ЃЌ ВЂИљОнМЦЫуНсЙћЃЌбЁдёКЯЪЪЕФЛиЙщФЃаЭНјааФтКЯЃЛ
ЂкИљОнЫљбЁЛиЙщФЃаЭЃЌЗжЮіЪлМлxЖЈЮЊЖрЩйЪБЃПРћШѓzПЩвдДяЕНзюДѓЃЎ
| | | |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
ЃЈИНЃКЯрЙижИЪ§  ЃЉ
ЃЉ