��Ŀ����
����Ŀ��ij��˾Ϊ�������״��������������1��������Ϊ5Ԫ/��������2����������Ϊ2Ԫ/��������ij��������Ӫ����������Ե㣨ÿ���Ե�����ֻ����һ�ִ����������������һ��Աȸõ�����һ��ȵ����������������Ӧ�ĵȸ�����ͼ��ͼ��ʾ�� 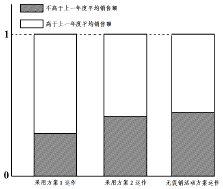
��1������ݵȸ�����ͼ�ṩ����Ϣ��Ϊ�ù�˾����ѡ��һ��Ϊ�����Ĵ��������������˵�����ɣ���
��2����֪�ù�˾��Ʒ�ijɱ�Ϊ10Ԫ/����δ����������������ã���Ϊ�ƶ�����ȸõ����IJ�Ʒ���ۼ۸�ͳ����һ��ȵ�8���ۼ�xi����λ��Ԫ/����������������yi����λ��������i=1��2������8�����±���ʾ��
�ۼ�x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
����y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
��������������ݼ�����Ӧ�����ָ��R2 �� �����ݼ�������ѡ����ʵĻع�ģ�ͽ�����ϣ�
�ڸ�����ѡ�ع�ģ�ͣ������ۼ�x��Ϊ����ʱ������z���Դﵽ���
| | | |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
���������ָ��  ��
��
���𰸡�
��1���⣺�ɵȸ�����ͼ��֪�����ƽ�����۶��뷽��1�����������ǿ�ڷ���2
��2���⣺������֪���ݿ�֪���ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
�ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
�ع�ģ�� ![]() ��Ӧ�����ָ��
��Ӧ�����ָ�� ![]() ��
��
��Ϊ ![]() �����Բ��ûع�ģ��
�����Բ��ûع�ģ�� ![]() ���������Ϊ���ʣ�
���������Ϊ���ʣ�
���ɣ�1����֪�����÷���1������Ч���Ϸ���2�ã�
�������� ![]() ��z'=����x+30����x��40����
��z'=����x+30����x��40����
��x�ʣ�0��40��ʱ�� ![]() ����������
����������
��x�ʣ�40��+�ޣ�ʱ�� ![]() �����ݼ���
�����ݼ���
�ʵ��ۼ�x=40ʱ������ﵽ���
����������1���ɵȸ�����ͼ��֪�����ƽ�����۶��뷽��1�����������ǿ�ڷ���2����2����������ָ�����ȽϿɵý��ۣ�
���ɣ�1����֪�����÷���1������Ч���Ϸ���2�ã��������� ![]() �����õ����ķ������ɵý��ۣ�
�����õ����ķ������ɵý��ۣ�

����Ŀ������ˮ���۾�˶�������ɫ�����������ž������С�����ˮ�������ݡ�֮��������ijˮ�ɻ����ʦ�ܹ�ÿ����250��ˮ�ɻ������ʦÿ���һ����1.2Ԫ��������ʦ���쳬������������IJ���ÿ��1.7Ԫ���������δ�ܰ������������ʵ����ɵĵ������ȡ���칤�ʣ� ��I������ʦ�������루��λ��Ԫ�����ڵ����n����λ������n��N���ĺ�������ʽf��n����
���õ��ʦ��¼�˹�ȥ10��ÿ��ĵ����n����λ�������������������
�����n | 210 | 230 | 250 | 270 | 300 |
Ƶ�� | 1 | 2 | 3 | 3 | 1 |
��10���¼�ĸ��������Ƶ����Ϊ������������ĸ��ʣ�
��������õ��ʦ��10���ƽ�����룻
��������õ��ʦ�������벻����300Ԫ�ĸ��ʣ�