题目内容
(本题满分12分)已知椭圆 过点
过点 ,且离心率为
,且离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ) 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 上异于
上异于
 的动点,直线
的动点,直线 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值.
 过点
过点 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)
 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值.(Ⅰ) . (Ⅱ)
. (Ⅱ) 为定值
为定值 .证明见解析。
.证明见解析。
 . (Ⅱ)
. (Ⅱ) 为定值
为定值 .证明见解析。
.证明见解析。 本试题主要是考出了椭圆方程的求解,椭圆的几何性质,直线与椭圆的位置关系的运用的综合考查,体现了运用代数的方法解决解析几何的本质的运用。
(1)首先根据题意的几何性质来表示得到关于a,b,c的关系式,从而得到其椭圆的方程。
(2设出直线方程,设点P的坐标,点斜式得到AP的方程,然后联立方程组,可知借助于韦达定理表示出长度,进而证明为定值。
(Ⅰ)解:由题意可知, ,
,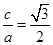 ,
,
解得 . …………4分
. …………4分
所以椭圆的方程为 . …………5分
. …………5分
(Ⅱ)证明:由(Ⅰ)可知, ,
, .设
.设 ,依题意
,依题意 ,
,
于是直线 的方程为
的方程为 ,令
,令 ,则
,则 .
.
即 . …………7分
. …………7分
又直线 的方程为
的方程为 ,令
,令 ,则
,则 ,
,
即 . …………9分
. …………9分
 …………11分
…………11分
又 在
在 上,所以
上,所以 ,即
,即 ,代入上式,
,代入上式,
得 ,所以
,所以 为定值
为定值 . …………12分
. …………12分
(1)首先根据题意的几何性质来表示得到关于a,b,c的关系式,从而得到其椭圆的方程。
(2设出直线方程,设点P的坐标,点斜式得到AP的方程,然后联立方程组,可知借助于韦达定理表示出长度,进而证明为定值。
(Ⅰ)解:由题意可知,
 ,
,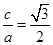 ,
,解得
 . …………4分
. …………4分所以椭圆的方程为
 . …………5分
. …………5分(Ⅱ)证明:由(Ⅰ)可知,
 ,
, .设
.设 ,依题意
,依题意 ,
,于是直线
 的方程为
的方程为 ,令
,令 ,则
,则 .
.即
 . …………7分
. …………7分又直线
 的方程为
的方程为 ,令
,令 ,则
,则 ,
,即
 . …………9分
. …………9分 …………11分
…………11分又
 在
在 上,所以
上,所以 ,即
,即 ,代入上式,
,代入上式,得
 ,所以
,所以 为定值
为定值 . …………12分
. …………12分
练习册系列答案
相关题目
 上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP,
上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB//OP, ,求椭圆的方程
,求椭圆的方程 与椭圆
与椭圆 相交于A、B两点.
相交于A、B两点. ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长; 与向量
与向量 互相垂直(其中O为坐标原点),当椭圆的离心率
互相垂直(其中O为坐标原点),当椭圆的离心率 时,求椭圆的长轴长的最大值.
时,求椭圆的长轴长的最大值.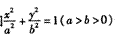 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2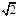 ,3-2
,3-2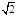
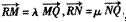 ,求证:
,求证: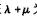 为定值.
为定值. 上的一点,点M、N分别是两圆:
上的一点,点M、N分别是两圆: 和
和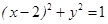 上的点,则的最小值、最大值分别为( )
上的点,则的最小值、最大值分别为( ) 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点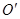 ),在斜平行光线的照射下,其阴影为一
),在斜平行光线的照射下,其阴影为一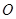 为原点,
为原点,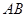 所在直线为
所在直线为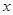 轴,设椭圆的方程为
轴,设椭圆的方程为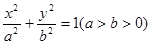 ,篮球与地面的接触点为
,篮球与地面的接触点为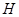 ,且
,且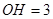 ,则椭圆的离心率为______.
,则椭圆的离心率为______.
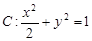 的左、右焦点分别为
的左、右焦点分别为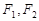 ,下顶点为
,下顶点为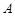 ,点
,点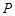 是椭圆上任一点,圆
是椭圆上任一点,圆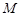 是以
是以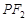 为直径的圆.
为直径的圆.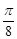 ,求
,求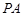 所在的直线方程;
所在的直线方程;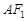 相切时,求圆
相切时,求圆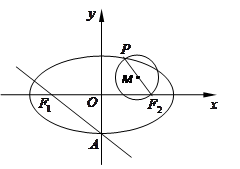
 与双曲线
与双曲线 有相同的焦点, 则m的值为( )
有相同的焦点, 则m的值为( )


