题目内容
已知椭圆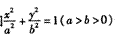 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2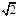 ,3-2
,3-2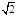
(1)求椭圆的方程;
(2)如果直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),证明直线CA与直线
BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,、若
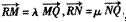 ,求证:
,求证: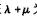 为定值.
为定值.
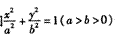 长轴上有一点到两个焦点之间的距离分别为:3+2
长轴上有一点到两个焦点之间的距离分别为:3+2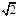 ,3-2
,3-2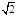
(1)求椭圆的方程;
(2)如果直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),证明直线CA与直线
BD的交点K必在一条确定的双曲线上;
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,、若
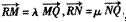 ,求证:
,求证: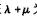 为定值.
为定值.(1)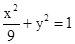 .(2)直线CA与直线BD的交点K必在双曲线
.(2)直线CA与直线BD的交点K必在双曲线 上
上
(3)λ+μ=- .
.
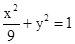 .(2)直线CA与直线BD的交点K必在双曲线
.(2)直线CA与直线BD的交点K必在双曲线 上
上(3)λ+μ=-
 .
. 本试题主要是考查了圆锥曲线方程的求解,以及直线与圆锥曲线的位置关系的综合运用。
(1)因为椭圆长轴上有一点到两个焦点之间的距离分别为:3+2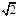 ,3-2
,3-2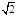 可知2a=6,a=3,然后结合a,b,c关系的得到椭圆的方程;
可知2a=6,a=3,然后结合a,b,c关系的得到椭圆的方程;
(2)因为 直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),要证明直线CA与直线BD的交点K必在一条确定的双曲线上;关键是表示出两条直线方程,然后得到证明。
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,联立方程组和韦达定理以及向量的关系式得到参数的关系式
(1)因为椭圆长轴上有一点到两个焦点之间的距离分别为:3+2
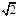 ,3-2
,3-2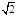 可知2a=6,a=3,然后结合a,b,c关系的得到椭圆的方程;
可知2a=6,a=3,然后结合a,b,c关系的得到椭圆的方程;(2)因为 直线x=t(teR)与椭圆相交于A,B,若C(-3,0),D(3,0),要证明直线CA与直线BD的交点K必在一条确定的双曲线上;关键是表示出两条直线方程,然后得到证明。
(3)过点Q(1,0 )作直线l(与x轴不垂直)与椭圆交于M,N两点,与y轴交于点R,联立方程组和韦达定理以及向量的关系式得到参数的关系式

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值. 离心率为
离心率为 ,且过点
,且过点 .
. 椭圆
椭圆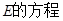
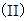 已知
已知
 直线
直线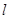 与椭圆
与椭圆 交于A、B两点,与
交于A、B两点,与 轴交于
轴交于 点,若
点,若 ,
, ,
, 的标准方程。
的标准方程。
 和
和 ,又过点
,又过点 .
. 在这个椭圆上,且
在这个椭圆上,且 ,求
,求 的余弦的大小.
的余弦的大小. 中,满足
中,满足 ,
, .若一个椭圆恰好以
.若一个椭圆恰好以 为一个焦点,另一个焦点在线段
为一个焦点,另一个焦点在线段 上,且
上,且 ,
, 均在此椭圆上,则该椭圆的离心率为 .
均在此椭圆上,则该椭圆的离心率为 . ,如果
,如果 的最小值为m,则满足
的最小值为m,则满足 的整点
的整点 的个数为 ( )
的个数为 ( ) 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0, ),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B 两点,且A、B两点与另一焦点围成的三角形周长为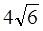 。
。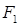 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, (O坐标原点),求直线m的方程
(O坐标原点),求直线m的方程 的离心率为
的离心率为 ,且过点Q(1,
,且过点Q(1,
 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值. ,
,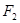 是椭圆
是椭圆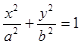
 左右焦点,它的离心率
左右焦点,它的离心率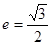 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为
 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求 的取值范围。
的取值范围。