题目内容
如图,已知椭圆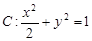 的左、右焦点分别为
的左、右焦点分别为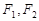 ,下顶点为
,下顶点为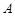 ,点
,点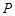 是椭圆上任一点,圆
是椭圆上任一点,圆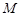 是以
是以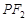 为直径的圆.
为直径的圆.
⑴当圆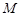 的面积为
的面积为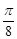 ,求
,求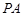 所在的直线方程;
所在的直线方程;
⑵当圆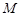 与直线
与直线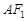 相切时,求圆
相切时,求圆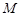 的方程;
的方程;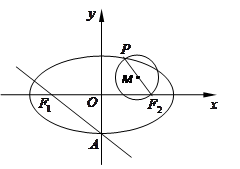
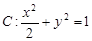 的左、右焦点分别为
的左、右焦点分别为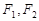 ,下顶点为
,下顶点为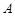 ,点
,点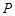 是椭圆上任一点,圆
是椭圆上任一点,圆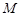 是以
是以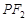 为直径的圆.
为直径的圆.⑴当圆
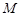 的面积为
的面积为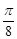 ,求
,求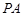 所在的直线方程;
所在的直线方程;⑵当圆
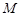 与直线
与直线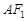 相切时,求圆
相切时,求圆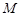 的方程;
的方程;
⑴ 或
或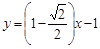 ;⑵
;⑵ ;
; 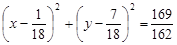 .
.
 或
或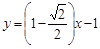 ;⑵
;⑵ ;
; 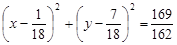 .
.(1) 设 ,先求出
,先求出 ,进而根椐圆
,进而根椐圆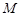 的面积为
的面积为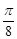 ,建立方程
,建立方程 ,解出
,解出 ,进而确定
,进而确定 或
或 .PA的直线方程易求.
.PA的直线方程易求.
(2) 直线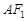 的方程为
的方程为 ,且
,且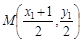 到直线
到直线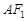 的距离为
的距离为
 ,得到
,得到 ,再根据点P在椭圆上满足
,再根据点P在椭圆上满足 ,两方程联立可得M的坐标,到此问题基本得到解决.
,两方程联立可得M的坐标,到此问题基本得到解决.
解:⑴易得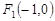 ,
,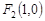 ,
, ,设
,设 ,
,
则 ,
,
∴ , ………………2
, ………………2
又圆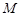 的面积为
的面积为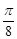 ,∴
,∴ ,解得
,解得 , ∴
, ∴ 或
或 ,
,
∴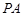 所在的直线方程为
所在的直线方程为 或
或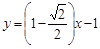 ;……………5
;……………5
⑵∵直线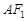 的方程为
的方程为 ,且
,且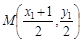 到直线
到直线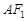 的距离为
的距离为
 , 化简得
, 化简得 ,………………………6
,………………………6
联立方程组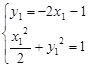 ,解得
,解得 或
或 . ………………………10
. ………………………10
当 时,可得
时,可得 , ∴ 圆
, ∴ 圆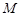 的方程为
的方程为 ;………11
;………11
当 时,可得
时,可得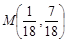 , ∴ 圆
, ∴ 圆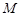 的方程为
的方程为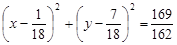 ;…12
;…12
 ,先求出
,先求出 ,进而根椐圆
,进而根椐圆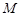 的面积为
的面积为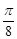 ,建立方程
,建立方程 ,解出
,解出 ,进而确定
,进而确定 或
或 .PA的直线方程易求.
.PA的直线方程易求.(2) 直线
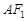 的方程为
的方程为 ,且
,且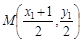 到直线
到直线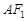 的距离为
的距离为 ,得到
,得到 ,再根据点P在椭圆上满足
,再根据点P在椭圆上满足 ,两方程联立可得M的坐标,到此问题基本得到解决.
,两方程联立可得M的坐标,到此问题基本得到解决.解:⑴易得
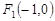 ,
,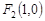 ,
, ,设
,设 ,
,则
 ,
,∴
 , ………………2
, ………………2又圆
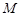 的面积为
的面积为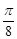 ,∴
,∴ ,解得
,解得 , ∴
, ∴ 或
或 ,
,∴
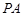 所在的直线方程为
所在的直线方程为 或
或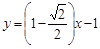 ;……………5
;……………5⑵∵直线
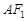 的方程为
的方程为 ,且
,且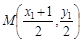 到直线
到直线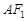 的距离为
的距离为 , 化简得
, 化简得 ,………………………6
,………………………6联立方程组
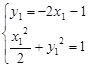 ,解得
,解得 或
或 . ………………………10
. ………………………10当
 时,可得
时,可得 , ∴ 圆
, ∴ 圆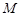 的方程为
的方程为 ;………11
;………11当
 时,可得
时,可得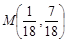 , ∴ 圆
, ∴ 圆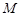 的方程为
的方程为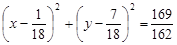 ;…12
;…12
练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值.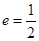 ,过左焦点
,过左焦点 作直线
作直线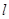 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线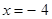 交于点
交于点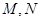 .
.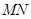 为直径的圆经过焦点
为直径的圆经过焦点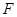 .
. ,
,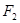 是椭圆
是椭圆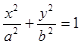
 左右焦点,它的离心率
左右焦点,它的离心率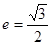 ,且被直线
,且被直线 所截得的线段的中点的横坐标为
所截得的线段的中点的横坐标为
 是其椭圆上的任意一点,当
是其椭圆上的任意一点,当 为钝角时,求
为钝角时,求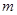 的取值范围。
的取值范围。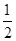 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心. ,且经过点
,且经过点 ,过椭圆的左焦点作直线
,过椭圆的左焦点作直线 交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。 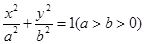 的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,
的右焦点,过原点的直线交椭圆于点A、P,PF垂直于x轴,直线AF交椭圆于点B,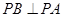 ,则该椭圆的离心率
,则该椭圆的离心率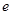 =___▲___.
=___▲___.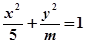 的离心率为
的离心率为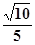 ,则实数
,则实数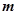 的值为___________.
的值为___________. 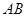 是椭圆
是椭圆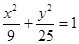 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,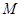 为
为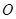 为坐标原点,则
为坐标原点,则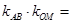 ____________
____________