题目内容
4．设a，b∈R+，求证：$\frac{a}{1+a}$+$\frac{b}{1+b}$＞$\frac{a+b}{1+a+b}$．分析 利用放缩法，即可证明结论．
解答 证明：∵a，b∈R+，
∴$\frac{a}{1+a}$＞$\frac{a}{1+a+b}$，$\frac{b}{1+b}$＞$\frac{b}{1+a+b}$，
∴$\frac{a}{1+a}$+$\frac{b}{1+b}$＞$\frac{a+b}{1+a+b}$．
点评 本题考查不等式的证明，考查放缩法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目
14．某商场2014年一月份到十二月份销售额呈现先下降后上升的趋势，下列函数模型中能较准确反映该商场月销售额f（x）与月份x关系的是（ ）
| A． | f（x）=a•bn（b＞0，且b≠1） | B． | f（x）=lognx+b（a＞0，且a≠1） | ||
| C． | f（x）=x2+ax+b | D． | f（x）=$\frac{a}{x}+b$ |
如图，四棱锥P-ABCD中，PA⊥平面ABCD，ABCD为正方形，则该四棱锥中互相垂直的平面有6组．
9．
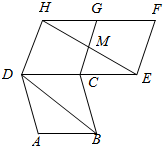如图，四边形ABCD，CEFG，CGFD都是全等的菱形，HE与CG相交于点M，则下列关系不一定成立的是（ ）
如图，四边形ABCD，CEFG，CGFD都是全等的菱形，HE与CG相交于点M，则下列关系不一定成立的是（ ）| A． | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B． | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C． | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D． | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
13．化简：$\sqrt{1-2sin（π-2）•cos（π-2）}$得（ ）
| A． | sin2+cos2 | B． | cos2-sin2 | C． | sin2-cos2 | D． | ±（cos2-sin2） |
如图，椭圆 M：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，直线x=±a和y=±b所围成的矩形 A BCD的面积为$32\sqrt{3}$．