题目内容
9.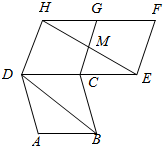 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |
分析 根据题意,结合菱形的四条边长相等,对边互相平行,分别对四个选项进行判断即可.
解答 解:根据题意,菱形的边长相等,∴|$\overrightarrow{AB}$|=|$\overrightarrow{EF}$|,A正确;
又菱形的对边平行,∴$\overrightarrow{AB}$与$\overrightarrow{FH}$共线,B正确;
若$\overrightarrow{BD}$与$\overrightarrow{EH}$共线时,BD∥EH,∠BDC=∠HEC,
显然不成立,∴$\overrightarrow{BD}$与$\overrightarrow{EH}$不共线,C错误;
又DC∥HG,CE∥HG,
∴DC∥CE,∴$\overrightarrow{DC}$与$\overrightarrow{EC}$共线,D正确.
故选:C.
点评 本题考查了平面向量共线的判断问题,也考查了菱形性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2)}\\{-\frac{1}{2}{x}^{2}+4x-7,x∈[2,+∞)}\end{array}\right.$,则关于x的方程f(x)=a(0<a<1)的所有根之和为( )
| A. | 3-a-1 | B. | 1-3-a | C. | 3a-1 | D. | 1-3a |
15.函数 f(x)=ex+a,g(x)=|ln(-x)|,若x1,x2都满足f(x)=g(x),则( )
| A. | x1•x2>e | B. | 1<x1•x2<e | C. | 0<x1x2<$\frac{1}{e}$ | D. | $\frac{1}{e}<{x_1}{x_2}$<1 |