题目内容
20．如图是一个几何体的三视图，则这个几何体的体积为（ ）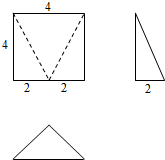
| A． | $\frac{16}{3}$ | B． | $\frac{32}{3}$ | C． | $\frac{64}{3}$ | D． | 16 |
分析 根据几何体的三视图，得出该几何体是直四棱锥，结合图中数据即可求出它的体积．
解答 解：根据几何体的三视图，得；
该几何体是直四棱锥，
且四棱锥的底面是边长为4的正方形，高为2，
则该四棱锥的体积为
V=$\frac{1}{3}$×42×2
=$\frac{32}{3}$．
故选：B．
点评 本题考查了空间几何体三视图的应用问题，也考查了空间想象能力与计算能力的应用问题，是基础题目．
练习册系列答案
相关题目
10．正四棱锥V-ABCD的侧棱长与底面边长相等，E是VA中点，O是底面中心，则异面直线EO与BC所成的角是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
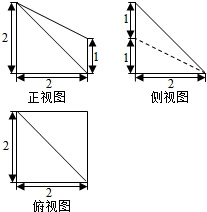
8．
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）| A． | $\sqrt{3}$+4 | B． | $\sqrt{3}$+6 | C． | 2$\sqrt{3}$+4 | D． | 2$\sqrt{3}$+6 |
5．三棱锥的高为3，底面是边长为3的正三角形，则这个三棱锥的体积是（ ）
| A． | $\frac{27}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{27\sqrt{3}}{4}$ | D． | $\frac{9\sqrt{3}}{4}$ |
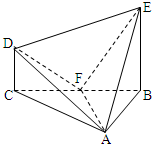在几何体ABCDE中，∠BAC=$\frac{π}{2}$，DC⊥平面ABC，EB⊥平面ABC，AB=AC=BE=2，CD=1，设F是BC的中点．