题目内容
11.斜率为1的直线与双曲线2x2-y2=1相交于A、B两点,又AB中点的横坐标为2.(Ⅰ)求直线的方程
(Ⅱ)求线段AB的长.
分析 (Ⅰ)设出直线方程,代双曲线方程,利用韦达定理及AB中点的横坐标为1,求出m,即可求直线的方程;
(Ⅱ)利用弦长公式,即可求得线段AB的长.
解答 解:(Ⅰ)设斜率为1的直线l的方程为y=x+m,代入2x2-y2=1,消去y可得x2-2mx-(m2+1)=0,
∴△=8m2+4>0,
设A(x1,y1),B(x2,y2),则x1+x2=2m,x1x2=-(m2+1),
∵AB中点的横坐标为1,
∴x1+x2=2m=4,
∴m=2,
∴直线的方程为y=x+2;
(Ⅱ)x1+x2=4,x1x2=-5,
∴|AB|=$\sqrt{2}$•$\sqrt{16+20}$=6$\sqrt{2}$.
点评 本题考查直线与双曲线的位置关系,考查韦达定理及弦长公式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
6.已知双曲线的中心在原点,焦点在x轴上,若其渐进线与圆x2+y2-6y+3=0相切,则此双曲线的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{6}$ |
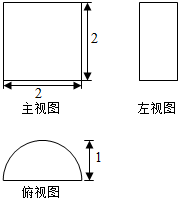
3.某空间几何体的三视图(单位:cm)如图所示,则此几何体的体积为( )


| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
20.如图是一个几何体的三视图,则这个几何体的体积为( )
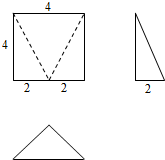

| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
 如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)
如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)