题目内容
5．三棱锥的高为3，底面是边长为3的正三角形，则这个三棱锥的体积是（ ）| A． | $\frac{27}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{27\sqrt{3}}{4}$ | D． | $\frac{9\sqrt{3}}{4}$ |
分析 直接运用体积公式求解即可．
解答 解：∵一个正三棱锥的三棱锥的高为3，底面是边长为3的正三角形，
∴这个正三棱锥的体积为$\frac{1}{3}×$$\frac{\sqrt{3}}{4}$×32×3=$\frac{9\sqrt{3}}{4}$，
故选：D．
点评 本题考查了空间几何体的体积公式，属于计算题，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
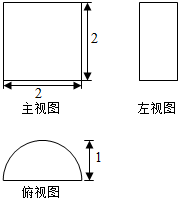
15．
各棱长都为2的四棱锥，底面ABCD是正方形，将侧面PBC水平放置，则这个几何体的俯视图的面积为（ ）
各棱长都为2的四棱锥，底面ABCD是正方形，将侧面PBC水平放置，则这个几何体的俯视图的面积为（ ）| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{4\sqrt{3}}{3}$ | D． | $\frac{5\sqrt{3}}{3}$ |
已知椭圆C的中心在原点，一个焦点和抛物线y2=8x的焦点重合，离心率等于$\frac{1}{2}$．
20．如图是一个几何体的三视图，则这个几何体的体积为（ ）
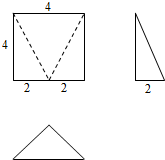
| A． | $\frac{16}{3}$ | B． | $\frac{32}{3}$ | C． | $\frac{64}{3}$ | D． | 16 |
17．函数y=ax+3-2（a＞0，a≠1）的图象恒过定点A，若点A在直线$\frac{x}{m}+\frac{y}{n}$=-1上，m＞0，n＞0，则3m+n的最小值为（ ）
| A． | 13 | B． | 16 | C． | 11+6$\sqrt{2}$ | D． | 28 |