题目内容
12.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≤0)}\\{{x}^{\frac{1}{2}}(x>0)}\end{array}\right.$,若f(a)>3,则a的取值范围是(9,+∞).分析 讨论当a≤0时,当a>0时,运用指数函数和幂函数的单调性,解不等式即可得到所求范围.
解答 解:当a≤0时,2a-1>3,解得a>2,不成立;
当a>0时,${a}^{\frac{1}{2}}$>3,解得a>9.
综上可得a>9.
故答案为:(9,+∞).
点评 本题考查分段函数的运用:解不等式,考查指数函数和幂函数的单调性,考查运算能力,属于基础题.

练习册系列答案
相关题目
3.某空间几何体的三视图(单位:cm)如图所示,则此几何体的体积为( )
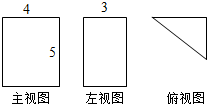

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
20.如图是一个几何体的三视图,则这个几何体的体积为( )
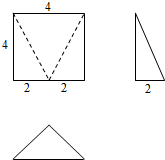

| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
7.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是( )
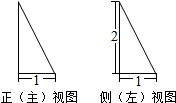

| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
17.函数y=ax+3-2(a>0,a≠1)的图象恒过定点A,若点A在直线$\frac{x}{m}+\frac{y}{n}$=-1上,m>0,n>0,则3m+n的最小值为( )
| A. | 13 | B. | 16 | C. | 11+6$\sqrt{2}$ | D. | 28 |
4.“实系数一元二次方程x2+x+c=0有虚根”是“c>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
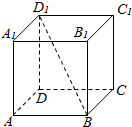 如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)
如图,在正方形ABCD-A1B1C1D1中,若平面a平行于该正方体的体对角线BD,则平面a在该正方体上截得的图形不可能为②③④(填序号)