题目内容
8. 一个空间几何体的三视图如图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为( )
一个空间几何体的三视图如图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为( )| A. | $\sqrt{3}$+4 | B. | $\sqrt{3}$+6 | C. | 2$\sqrt{3}$+4 | D. | 2$\sqrt{3}$+6 |
分析 由已知中的三视力可得该几何体是一个四棱锥,计算出各个侧面的面积,相加可得答案.
解答 解:由已知中的三视力可得该几何体是一个四棱锥,
其直观图如下图所示: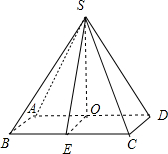
则△SAD是边长为2的正三角形,其面积为:$\sqrt{3}$,
∵AB⊥平面SAD,可得:△SAB是两直角边长为1和2的直角三角形,
故△SAB的面积为1,
同理,△SCD的面积也为1,
又由△SAD的高SO=$\sqrt{3}$,OE=AB=1,可得SE=2,
故△SBC是底边长2,高为2的等腰三角形,故△SBC的面积为2,
综上所述,几何体的侧面积为$\sqrt{3}$+4,
故选:A
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
3.某空间几何体的三视图(单位:cm)如图所示,则此几何体的体积为( )
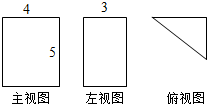

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
20.如图是一个几何体的三视图,则这个几何体的体积为( )
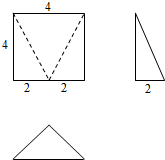

| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
17.函数y=ax+3-2(a>0,a≠1)的图象恒过定点A,若点A在直线$\frac{x}{m}+\frac{y}{n}$=-1上,m>0,n>0,则3m+n的最小值为( )
| A. | 13 | B. | 16 | C. | 11+6$\sqrt{2}$ | D. | 28 |
18.若方程${(\frac{1}{4})^x}+{(\frac{1}{2})^{x-1}}$-a=0有正数解,则实数a的取值范围是( )
| A. | 0<a<1 | B. | -3<a<0 | C. | 0<a<3 | D. | -1<a<0 |
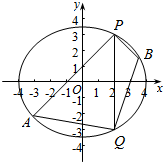 已知椭圆C的中心在原点,一个焦点和抛物线y2=8x的焦点重合,离心率等于$\frac{1}{2}$.
已知椭圆C的中心在原点,一个焦点和抛物线y2=8x的焦点重合,离心率等于$\frac{1}{2}$.