题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 两个极值点
两个极值点![]() ,试判断
,试判断![]() 与
与![]() 的大小关系并证明.
的大小关系并证明.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析
,证明见解析
【解析】
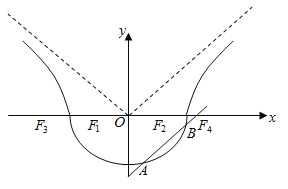
(1)利用函数有两个极值点可知![]() 在
在![]() 上有两个不等实根,将问题转化为
上有两个不等实根,将问题转化为![]() 与
与![]() 在
在![]() 有两个不同的交点的问题,通过数形结合的方式确定相切为临界状态,进而利用过某点处切线的求解方法可求得结果;
有两个不同的交点的问题,通过数形结合的方式确定相切为临界状态,进而利用过某点处切线的求解方法可求得结果;
(2)根据![]() 为
为![]() 的两根可得到
的两根可得到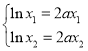 ,设
,设![]() ,则
,则![]() ,由方程组可求得
,由方程组可求得![]() ,将
,将![]() 与
与![]() 的大小比较问题转化为比较
的大小比较问题转化为比较![]() 的大小关系,进一步将问题化为比较
的大小关系,进一步将问题化为比较![]() 大小关系,设
大小关系,设![]() ,利用导数可求得
,利用导数可求得![]() ,进而得到结论.
,进而得到结论.
(1)由题意得:![]() 定义域为
定义域为![]() ,
,![]() ,
,
![]() 有两个极值点,
有两个极值点,![]() 在
在![]() 上有两个不等实根,
上有两个不等实根,
令![]() ,则
,则![]() 与
与![]() 在
在![]() 有两个不同的交点,
有两个不同的交点,
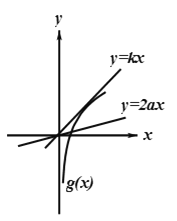
当![]() 与
与![]() 相切时,设切点为
相切时,设切点为![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
则当![]() 时,
时,![]() 与
与![]() 在
在![]() 有两个不同的交点,
有两个不同的交点,![]() ,
,
即当![]() 时,
时,![]() 有两个极值点.
有两个极值点.
(2)![]() ,证明如下:
,证明如下:
由题意得:![]() ,
,
![]() 为
为![]() 的两个根,不妨设
的两个根,不妨设![]() ,则
,则![]() ,
,
则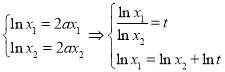 ,解得:
,解得:![]() ,
,
要考虑![]() 大小关系即考虑
大小关系即考虑![]() 的大小关系,
的大小关系,
即考虑![]() 的大小关系即考虑
的大小关系即考虑![]() 的大小关系,
的大小关系,
即考虑![]() 的大小关系即
的大小关系即![]() 的大小关系,
的大小关系,
令![]() ,
,
则![]() ,
,
由![]() 知:
知:![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,即
,即![]() ,
,
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: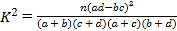 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】保护环境就是保护人类健康.空气中负离子浓度(单位:个/![]() )可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表
)可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表![]() .
.
表![]() 负离子浓度与空气质量对应标准:
负离子浓度与空气质量对应标准:
负离子浓度 | 等级 | 和健康的关系 |
|
| 不利 |
|
| 正常 |
|
| 较有利 |
|
| 有利 |
|
| 相当有利 |
|
| 很有利 |
|
| 极有利 |
图![]() 空气负离子浓度
空气负离子浓度
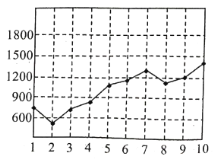
某地连续![]() 天监测了该地空气负离子浓度,并绘制了如图
天监测了该地空气负离子浓度,并绘制了如图![]() 所示的折线图.根据折线图,下列说法错误的是( )
所示的折线图.根据折线图,下列说法错误的是( )
A.这![]() 天的空气负离子浓度总体越来越高
天的空气负离子浓度总体越来越高
B.这![]() 天中空气负离子浓度的中位数约
天中空气负离子浓度的中位数约![]() 个
个![]()
C.后![]() 天的空气质量对身体健康的有利程度明显好于前
天的空气质量对身体健康的有利程度明显好于前![]() 天
天
D.前![]() 天空气质量波动程度小于后
天空气质量波动程度小于后![]() 天
天