题目内容
【题目】如图，在四棱锥P－ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝
，PA＝AD＝2，AB＝BC＝1，点M、E分别是PA、PD的中点
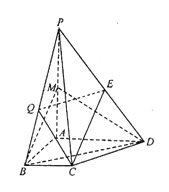
(1)求证：CE//平面BMD
(2)点Q为线段BP中点，求直线PA与平面CEQ所成角的余弦值.
【答案】(1)见解析；（2）
.
【解析】
(1) 连接ME，通过对边关系得到四边形
为平行四边形，所以
，进而得到线面平行；（2）建立坐标系，进而得到直线PA的方向向量，和面的法向量，进而得到线面角.
（1）连接ME，因为点
分别是
的中点，所以
，所以
，所以四边形为平行四边形，所以.又因为
平面
，
平面,所以
平面.
（2）如图，以
为坐标原点建立空间坐标系
，则
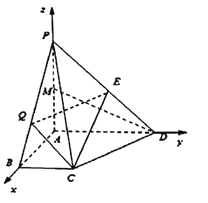
又
，
设平面
的法向量为
，列方程组求得其中一个法向量为
，设直线
与平面所成角大小为
，于是
，
进而求得.
练习册系列答案
阅读快车系列答案
相关题目
【题目】健身馆某项目收费标准为每次60元，现推出会员优惠活动：具体收费标准如下：
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数，得到数据如下：
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元，根据给出的数据回答下列问题：
（1）估计1位会员至少消费两次的概率
（2）某会员消费4次，求这4次消费获得的平均利润；
