题目内容
【题目】已知函数![]() (m
(m![]() R)的导函数为
R)的导函数为![]() .
.
(1)若函数![]() 存在极值,求m的取值范围;
存在极值,求m的取值范围;
(2)设函数![]() (其中e为自然对数的底数),对任意m
(其中e为自然对数的底数),对任意m![]() R,若关于x的不等式
R,若关于x的不等式![]() 在(0,
在(0,![]() )上恒成立,求正整数k的取值集合.
)上恒成立,求正整数k的取值集合.
【答案】(1)![]() (2){1,2}.
(2){1,2}.
【解析】
(1)求解导数,表示出![]() ,再利用
,再利用![]() 的导数可求m的取值范围;
的导数可求m的取值范围;
(2)表示出![]() ,结合二次函数知识求出
,结合二次函数知识求出![]() 的最小值,再结合导数及基本不等式求出
的最小值,再结合导数及基本不等式求出![]() 的最值,从而可求正整数k的取值集合.
的最值,从而可求正整数k的取值集合.
(1)因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
则![]() ,
,
由题意可知![]() ,解得
,解得![]() ;
;
(2)由(1)可知,![]() ,
,
所以![]()
因为![]()
整理得![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 单调递增,
单调递增,
又因为![]() ,
,
所以存在![]() ,使得
,使得![]() ,
,
设![]() ,是关于
,是关于![]() 开口向上的二次函数,
开口向上的二次函数,
则![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 单调递增,因为
单调递增,因为![]() ,
,![]()
所以存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又由题意可知![]() ,所以
,所以![]() ,
,
解得![]() ,所以正整数k的取值集合为{1,2}.
,所以正整数k的取值集合为{1,2}.

 阅读快车系列答案
阅读快车系列答案【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: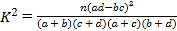 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?