题目内容
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与![]() 的人机大战中中盘弃子认输,至此柯洁与
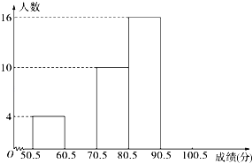
的人机大战中中盘弃子认输,至此柯洁与![]() 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

(1)请根据已知条件完成下面![]() 列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)为了进一步了解“围棋迷”的围棋水平,从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛,首轮该校需派两名学生出赛,若从5名学生中随机抽取2人出赛,求2人恰好一男一女的概率.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据频率分布直方图可计算出在抽取的100人中,“围棋迷”有25人,即可完成表格,计算![]() 的值可得结果;(2)按照分层抽样性质可得抽取的5名学生中,有男生3名,有女生2名利用列举法结合古典概型概率计算公式可得结果.
的值可得结果;(2)按照分层抽样性质可得抽取的5名学生中,有男生3名,有女生2名利用列举法结合古典概型概率计算公式可得结果.
试题解析:(1)由频率分布直方图可知, ![]()
所以在抽取的100人中,“围棋迷”有25人,
从而![]() 列联表如下
列联表如下
非围棋迷 | 围棋迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
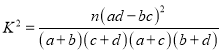
![]()
因为![]() ,所以没有95%的把握认为“围棋迷”与性别有关.
,所以没有95%的把握认为“围棋迷”与性别有关.
(2)由(1)中列联表可知25名“围棋迷”中有男生15名,女生10名,所以从“围棋迷”中按性别分层抽样抽取的5名学生中,有男生3名,记为![]() ,有女生2名,记为
,有女生2名,记为![]() ,则从5名学生中随机抽取2人出赛,基本事件有:
,则从5名学生中随机抽取2人出赛,基本事件有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10种; 其中2人恰好一男一女的有:
,共10种; 其中2人恰好一男一女的有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共6种;
,共6种;
故2人恰好一男一女的概率为![]() .
.

【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 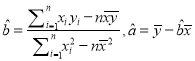 .
.