题目内容
【题目】已知圆![]() ,点
,点![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ) ![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 经过定点
经过定点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ,若存在,请求出定点
,若存在,请求出定点![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ) 存在定点
;(Ⅱ) 存在定点![]() .
.
【解析】试题分析:(1)由两圆内切,圆心距等于半径差,可知动圆圆心S到O与F的距离和为定值2,取![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,由中位线可知
,由中位线可知![]() ,所以点
,所以点![]() 的轨迹是以
的轨迹是以![]() ,
, ![]() 为焦点,长轴长为4的椭圆。(2)由得
为焦点,长轴长为4的椭圆。(2)由得![]() ,得直线得
,得直线得![]() 与
与![]() 斜率和为零.设
斜率和为零.设![]() ,
, ![]() ,直线
,直线![]() 的方程为
的方程为![]() 得
得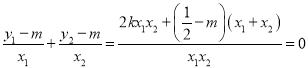 ,代入韦达可求。
,代入韦达可求。
试题解析:(Ⅰ)设![]() 的中点为
的中点为![]() ,切点为
,切点为![]() ,连
,连![]() ,则
,则![]() ,取
,取![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() ,故
,故![]() .
.
所以点![]() 的轨迹是以
的轨迹是以![]() ,
, ![]() 为焦点,长轴长为4的椭圆.
为焦点,长轴长为4的椭圆.
其中, ![]() 曲线
曲线![]() 方程为
方程为![]() .
.
(Ⅱ)假设存在满足题意的定点![]() ,设
,设![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
, ![]() .由
.由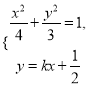 消去
消去![]() ,得
,得![]()
由直线![]() 过椭圆内一点
过椭圆内一点![]() 作直线故
作直线故![]() ,由求根公式得:
,由求根公式得:
![]()
由得![]() ,得直线得
,得直线得![]() 与
与![]() 斜率和为零.故
斜率和为零.故
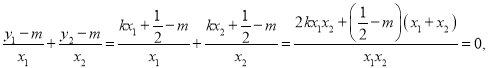
![]()
存在定点![]() ,当斜率不存在时定点
,当斜率不存在时定点![]() 也符合题意.
也符合题意.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
【题目】2017年5月27日当今世界围棋排名第一的柯洁在与![]() 的人机大战中中盘弃子认输,至此柯洁与
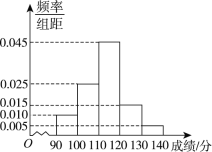
的人机大战中中盘弃子认输,至此柯洁与![]() 的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
的三场比赛全部结束,柯洁三战全负,这次人机大战再次引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查,根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

(1)请根据已知条件完成下面![]() 列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
列联表,并据此资料你是否有95%的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)为了进一步了解“围棋迷”的围棋水平,从“围棋迷”中按性别分层抽样抽取5名学生组队参加校际交流赛,首轮该校需派两名学生出赛,若从5名学生中随机抽取2人出赛,求2人恰好一男一女的概率.