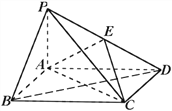
题目内容
【题目】在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=![]() ,EF=1,BC=
,EF=1,BC=![]() ,且M是BD的中点。
,且M是BD的中点。

(1)求证:EM∥平面ADF;
(2)求二面角D-AF-B的余弦值;
(3)在线段ED上是否存在一点P,使得BP∥平面ADF?若存在,求出EP的长度;若不存在,请说明理由。
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)取AD的中点N,连接MN、NF.由三角形中位线定理,结合已知条件,证出四边形MNFE为平行四边形,从而得到EM∥FN,结合线面平行的判定定理,证出EM∥平面ADF;
(2)建立如图所示的空间直角坐标系B-xyz,求出平面ADF、平面EBAF的一个法向量,利用向量的夹角公式,可求二面角D﹣AF﹣B的大小;
(3)假设在线段ED上存在一点P,使得BP与平面ADF平行,利用向量法即可得到结果.
(1)取AD的中点N,连接MN,NF。
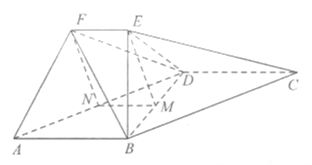
在△DAB中,M是BD的中点,N是AD的中点,所以MN∥AB,MN=![]() AB,
AB,
又因为EF∥AB,EF=![]() AB,
AB,
所以MN∥EF且MN=EF,
所以四边形MNFE为平行四边形,
所以EM∥FN,
又因为FN![]() 平面ADF,EM
平面ADF,EM![]() 平面ADF,
平面ADF,
故EM∥平面ADF。
解法二:因为EB⊥平面ABD,AB⊥BD,故以B为原点,
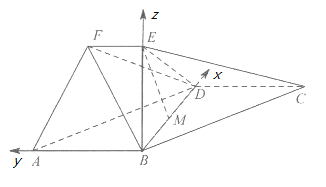
建立如图所示的空间直角坐标系B-xyz。
由已知可得B(0,0,0),A(0,2,0),D(3,0,0),C(3,-2,0),
E(0,0,![]() ),F(0,1,
),F(0,1,![]() ),M(
),M(![]() ,0,0)。
,0,0)。
(1)![]() =(
=(![]() ,0,
,0,![]() ),
),![]() =(3,-2,0),
=(3,-2,0),![]() =(0,-1,
=(0,-1,![]() )。
)。
设平面ADF的一个法向量是![]()
由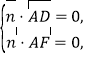 得
得![]()
令![]() ,则
,则![]() =(2,3,
=(2,3,![]() )。
)。
又因为![]() ·
·![]() =(
=(![]() ,0,
,0,![]() )·(2,3,
)·(2,3,![]() )=3+0-3=0,
)=3+0-3=0,
所以![]() ⊥
⊥![]() ,又EM
,又EM![]() 平面ADF,所以EM∥平面ADF。
平面ADF,所以EM∥平面ADF。
(2)由(1)可知平面ADF的一个法向量是![]() =(2,3,
=(2,3,![]() )因为EB⊥平面ABD,所以EB⊥BD,
)因为EB⊥平面ABD,所以EB⊥BD,
又因为AB⊥BD,所以BD⊥平面EBAF,故![]() =(3,0,0)是平面EBAF的一个法向量,
=(3,0,0)是平面EBAF的一个法向量,
所以![]() >=
>=![]() ,又二面角D-AF-B为锐角,故二面角D-AF-B的余弦值为
,又二面角D-AF-B为锐角,故二面角D-AF-B的余弦值为![]() 。
。
(3)假设在线段ED上存在一点P,使得BP与平面ADF平行。
不妨设![]() =
=![]()
![]() =(3
=(3![]() ,0,-
,0,-![]()
![]() )(0≤
)(0≤![]() ≤1),
≤1),
则![]() =(3
=(3![]() ,0,3-
,0,3-![]()
![]() )。所以
)。所以![]() ·n=6
·n=6![]() +0+3
+0+3![]() -3
-3![]() =0,
=0,
由题意得![]() =
=![]() <0,所以在线段ED上不存在点P,使得BP与平面ADF平行。
<0,所以在线段ED上不存在点P,使得BP与平面ADF平行。

 名校课堂系列答案
名校课堂系列答案【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。