题目内容
【题目】设![]() ,关于
,关于![]() 的方程
的方程![]() ,给出下列四个命题,其中假命题的个数是( )
,给出下列四个命题,其中假命题的个数是( )
①存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
②存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
③存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根;
个不同的实根;
④存在实数![]() ,使得方程恰有
,使得方程恰有![]() 个不同的实根.
个不同的实根.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
作出函数图象,令![]() ,对根的判别式分类讨论即可得解.
,对根的判别式分类讨论即可得解.
解:![]()
可作函数图象如下所示:
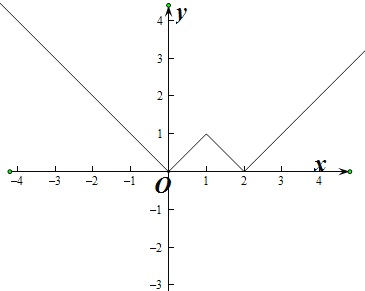
令![]() ,
,![]()
(1)当![]() 时,解得
时,解得![]() 或
或![]()
①当![]() 时,
时,![]() 解得
解得![]() 由图可知,存在
由图可知,存在![]() 个不同的实数使得
个不同的实数使得![]() ,
,
即方程![]() 有
有![]() 个不同的实数根;
个不同的实数根;
②当![]() 时,
时,![]() 解得
解得![]() 由图可知,不存在实数使得
由图可知,不存在实数使得![]() ,即方程
,即方程![]() 无实数根;
无实数根;
(2)当![]() 时,解得
时,解得![]() 或
或![]() ,
,
①当![]() 时,方程
时,方程![]() 有两不相等的实数根,设为
有两不相等的实数根,设为![]() ,
,![]() ,
,
则![]() ,
,![]()
![]() ,
,![]() 均为负数,由函数图象知
均为负数,由函数图象知![]() ,故不存在实数使得
,故不存在实数使得![]() ,即方程
,即方程![]() 无实数根;
无实数根;
②当![]() 时,方程
时,方程![]() 有两不相等的实数根,设为
有两不相等的实数根,设为![]() ,
,![]() ,
,
则![]() ,
,![]()
![]() ,
,![]() 均为正数且
均为正数且![]() ,
,
设![]() 则
则![]() ,由图可知,存在
,由图可知,存在![]() 个不同的实数使得
个不同的实数使得![]() ,
,
存在![]() 个不同的实数使得
个不同的实数使得![]() ,
,
即方程![]() 有
有![]() 个不同的实数根;
个不同的实数根;
(3)当![]() 时,方程无解,则方程
时,方程无解,则方程![]() 无实数根;
无实数根;
综上可得正确的有①④,错误的有②③
故选:![]()

【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有6人 | 6 | 6 | 3 | 1 | 2 | 0 |
选考方案待确定的有8人 | 5 | 4 | 0 | 1 | 2 | 1 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 0 | 0 | 1 | 1 |
(Ⅰ)试估计该学校高一年级确定选考生物的学生有多少人?
(Ⅱ)写出选考方案确定的男生中选择“物理、化学和地理”的人数.(直接写出结果)
(Ⅲ)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.


